problem
stringlengths 17
4.31k
| solution_hint
stringlengths 49
6.77k
| answer
stringlengths 1
44
⌀ | problem_type
stringclasses 8
values | source
stringclasses 2
values | level
stringclasses 3
values | type
stringclasses 7
values | solution
stringlengths 13
56
|
|---|---|---|---|---|---|---|---|
1. Find the sum of all roots of the equation:
$$
\begin{gathered}
\sqrt{2 x^{2}-2024 x+1023131}+\sqrt{3 x^{2}-2025 x+1023132}+\sqrt{4 x^{2}-2026 x+1023133}= \\
=\sqrt{x^{2}-x+1}+\sqrt{2 x^{2}-2 x+2}+\sqrt{3 x^{2}-3 x+3}
\end{gathered}
$$
(L. S. Korechkova)
|
Note that the radicands in the left part are obtained from the corresponding radicands in the right part by adding $x^{2}-2023 x+1023130=$ $(x-1010)(x-1013)$. Since all radicands are positive (it is sufficient to check for $x^{2}-x+1$ and for $\left.2 x^{2}-2024 x+1023131=2(x-506)^{2}+511059\right)$, the left part is less than the right part when $1010<x<1013$ and greater when $x \notin[1010,1013]$. Equality is achieved only at $x=1010$ and $x=1013$, so the answer is -2023.
Criteria. If the answer is found but it is not proven that there are no other roots of the equation, no more than 2 points.
|
-2023
|
Algebra
|
olympiads
| null | null |
\(\boxed{-2023}\)
|
5. A natural number $n$ is called cubish if $n^{3}+13 n-273$ is a cube of a natural number. Find the sum of all cubish numbers.
|
If $0<13n-273<13\cdot21$, so it remains to check all other numbers.
If $n=21$, then $13n-273=0$, so 21 is cubic. For $n-3n^{2}+3n-1$, the number $n$ will not be cubic (i.e., for $8<n<21$).
If $n=8$, then $13n-273=-169=-3\cdot8^{2}+3\cdot8-1$, so it is cubic. For $n \leqslant 5$, the expression $n^{3}+13n-273$ will be negative, so they are definitely not cubic. The numbers 6 and 7 are not cubic, which can be verified directly. In total, the answer is $8+21=29$.
|
29
|
Algebra
|
olympiads
| null | null |
\(\boxed{29}\)
|
1. A motorcyclist set out from point $A$ with an initial speed of 90 km/h, uniformly increasing his speed (that is, over equal time intervals, his speed increases by the same amount). After three hours, the motorcyclist arrived at point $B$, passing through $C$ along the way. After that, he turned around and, still uniformly increasing his speed, headed back. Two hours later, he passed point $C$ again at a speed of 110 km/h and continued on to $A$. Find the distance between points $A$ and $C$.
|
In 5 hours, the speed changed from 90 km/h to 110 km/h, so the acceleration is 4 km/h$^2$. From $A$ to $B$ the distance is
$$
90 \cdot 3+\frac{4}{2} \cdot 3^{2}=270+18=288(\text{km})
$$
from $B$ to $C-$
$$
110 \cdot 2-\frac{4}{2} \cdot 2^{2}=220-8=212(\text{km})
$$
And the required distance is 76 km.
|
76
|
Algebra
|
olympiads
| null | null |
\(\boxed{76}\)
|
6. A natural number $n$ is called cubish if $n^{3}+13 n-273$ is a cube of a natural number. Find the sum of all cubish numbers.
|
If $021$, so it remains to check all other numbers.
If $n=21$, then $13 n-273=0$, so 21 is cubic. For $n-3 n^{2}+3 n-1$, the number $n$ will not be cubic (i.e., for $8<n<21)$
If $n=8$, then $13 n-273=-169=-3 \cdot 8^{2}+3 \cdot 8-1$, so it is cubic. For $n \leqslant 5$, the expression $n^{3}+13 n-273$ will be negative, so they are definitely not cubic. The numbers 6 and 7 are not cubic, which can be verified directly. In total, the answer is $8+21=29$.
|
29
|
Number Theory
|
olympiads
| null | null |
\(\boxed{29}\)
|
1. In a certain language, there are 3 vowels and 5 consonants. A syllable can consist of any vowel and any consonant in any order, and a word can consist of any two syllables. How many words are there in this language?
|
The language has $3 \cdot 5=15$ syllables of the form "consonant+vowel" and the same number of syllables of the form "vowel+consonant", making a total of 30 different syllables. The total number of two-syllable words is $30 \cdot 30=900$
|
900
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{900}\)
|
3. Masha and Lena left home and went to the store for ice cream. Masha walked faster and got to the store in 12 minutes. Spending 2 minutes buying the ice cream, she headed back. After another 2 minutes, she met Lena. Walking a bit more, Masha finished her ice cream and, deciding to buy another one, turned around and went back to the store. As a result, Masha arrived at the store with Lena. How many minutes did Lena walk to the store?
|
Masha covers $1 / 6$ of the entire distance in 2 minutes, which means Lena covered $5 / 6$ of the distance by the time they met, and it took her 16 minutes. Therefore, $1 / 6$ of the distance takes Lena $16: 5=3 \frac{1}{5}$ minutes, i.e., 3 minutes and 12 seconds. For the entire distance, she would need 19 minutes and 12 seconds.
|
19
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{19}\)
|
1. Petya prints five digits on the computer screen, none of which are zeros. Every second, the computer removes the initial digit and appends to the end the last digit of the sum of the remaining four digits. (For example, if Petya enters 12345, after one second it will become 23454, then 34546, and so on. However, he can enter any five digits, not necessarily 12345.) At some point, Petya stops the process. What is the minimum possible sum of the five digits that could be on the screen at that moment?
(A. A. Tesler)
|
The record 00000 cannot appear on the screen, as it can only result from 00000. A record with four zeros and one also cannot appear, since in that case, the last digit would not equal the remainder of the division of the sum of the first four by 10.
However, a sum of digits equal to 2 is possible. For example, by working backwards, we can find an example of obtaining the record 00011 (or 10001):
$00011 \leftarrow 10001 \leftarrow 91000 \leftarrow 09100 \leftarrow 00910 \leftarrow 20091 \leftarrow 72009 \leftarrow 17200 \leftarrow 01720 \leftarrow 40172 \leftarrow$ $24017 \leftarrow 52401 \leftarrow 95240 \leftarrow 89524$.
Criteria. 5 points for the example, 2 points for the proof of the impossibility of smaller sums.
|
2
|
Number Theory
|
olympiads
| null | null |
\(\boxed{2}\)
|
1. In a certain language, there are 5 vowels and 7 consonants. A syllable can consist of any vowel and any consonant in any order, and a word can consist of any two syllables. How many words are there in this language?
|
The language has $5 \cdot 7=35$ syllables of the form "consonant+vowel" and the same number of syllables of the form "vowel+consonant", making a total of 70 different syllables. The total number of two-syllable words is $70 \cdot 70=4900$.
|
4900
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{4900}\)
|
1. In each cell of a $100 \times 100$ table, a natural number was written. It turned out that each number is either greater than all its neighbors or less than all its neighbors. (Two numbers are called neighbors if they are in cells sharing a common side.) What is the smallest value that the sum of all the numbers can take?
|
Let's divide the board into dominoes. In each domino, the numbers are different, so their sum is at least $1+2=3$. Then the total sum of the numbers on the board is at least 15000. This estimate is achievable if we alternate ones and twos in a checkerboard pattern.
|
15000
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{15000}\)
|
2. A company produces a certain product in the amount of $x_{1}$ in January, $x_{2}$ in February, $\ldots, x_{12}$ in December. The average production of the product from the beginning of the year is calculated as follows:
$x_{1}=x_{1}, \quad \bar{x}_{2}=\frac{1}{2}\left(x_{1}+x_{2}\right), \quad \bar{x}_{3}=\frac{1}{3}\left(x_{1}+x_{2}+x_{3}\right), \quad \ldots, \quad \bar{x}_{12}=\frac{1}{12}\left(x_{1}+x_{2}+\ldots+x_{12}\right)$.
It is known that $\bar{x}_{k}x_{k}$ for $k$ from 7 to 12. In which month was the average production of the product from the beginning of the year the highest?
|
Note that
\[
\begin{aligned}
\bar{x}_{k+1} & =\frac{1}{k+1}\left(x_{1}+x_{2}+\ldots+x_{k+1}\right)=\frac{1}{k+1}\left(k \bar{x}_{k}+x_{k+1}\right) \\
x_{k+1}-\bar{x}_{k+1} & =k\left(\bar{x}_{k+1}-\bar{x}_{k}\right)
\end{aligned}
\]
In total, we have found that the average production increases (decreases) when the production in the month is higher (lower) than the corresponding average. Therefore, the maximum was in the sixth month.
|
6
|
Algebra
|
olympiads
| null | null |
\(\boxed{6}\)
|
1. What is the maximum number of numbers that can be chosen from the set $\{1,2, \ldots, 12\}$ so that the product of no three chosen numbers is a perfect cube?
|
all except $4,9,12$. Note that to remove the cubes, we need to remove at least one element from each of the sets $\{1,2,4\},\{3,6,12\},\{2,4,8\},\{1,3,9\},\{2,9,12\}$, $\{3,8,9\},\{4,6,9\}$. Note that all numbers, except 9, are in no more than three of these seven triples. Therefore, if we remove two numbers different from 9, at least one triple will remain. If, however, we remove the number 9, then among the remaining triples there will be two non-intersecting $(\{1,2,4\},\{3,6,12\})$, so no matter which second number we remove, one of the triples will remain.
|
9
|
Number Theory
|
olympiads
| null | null |
\(\boxed{9}\)
|
11.1. Petya wrote a five-digit number on the board, consisting of different even digits. Vasya erased one digit so that the resulting number is divisible by 18. Which digit did Vasya erase?
|
The sum of the digits initially equals $0+2+4+6+8=20$. By erasing a digit, Vasya subtracts 0, 2, 4, 6, or 8 from the sum of the digits. The resulting number is divisible by 18, i.e., it is divisible by 9, which means the sum of its digits is divisible by 9. Therefore, Vasya can only erase 2 (otherwise, the sum of the digits will not be divisible by 9).
Criteria: Only the correct answer - 1 point. It is written that the sum of the digits must be divisible by 18 for the number to be divisible by $9(18)-5$ points.
|
2
|
Number Theory
|
olympiads
| null | null |
\(\boxed{2}\)
|
11.5. Given a function $f(x)$, satisfying the condition
$$
f(x y+1)=f(x) f(y)-f(y)-x+2
$$
What is $f(2017)$, if it is known that $f(0)=1$?
|
$f(0 \cdot 0+1)=f(0) f(0)-f(0)-0+2, f(1)=1-1+2=2$,
$$
f(2017 \cdot 0+1)=f(2017) f(0)-f(0)-2017+2
$$
$$
\begin{gathered}
f(1)=f(2017)-1-2017+2=2 \\
f(2017)=2018
\end{gathered}
$$
Criteria: Only for the correct answer - 1 point.
|
2018
|
Algebra
|
olympiads
| null | null |
\(\boxed{2018}\)
|
10.5. In a row, $n$ integers are written such that the sum of any three consecutive numbers is positive, while the sum of any five consecutive numbers is negative. For what largest $n$ is this possible
|
Let's provide an example for $n=6: 3,-5,3,3,-5,3$. We will prove that for $n \geq 7$ it will not be possible to write down a sequence of numbers that satisfy the condition of the problem. We will construct a table for the first 7 numbers in this sequence
| $a_{1}$ | $a_{2}$ | $a_{3}$ | $a_{4}$ | $a_{5}$ |
| :--- | :--- | :--- | :--- | :--- |
| $a_{2}$ | $a_{3}$ | $a_{4}$ | $a_{5}$ | $a_{6}$ |
| $a_{3}$ | $a_{4}$ | $a_{5}$ | $a_{6}$ | $a_{7}$ |
By the condition: the sum of the numbers in each row must be negative, and in each column positive. Therefore, the sum of all the numbers in the table should be positive on one side and negative on the other. Contradiction.
Criteria: Only for the correct answer - 1 point. Correct answer with an example - 2 points.
|
6
|
Number Theory
|
olympiads
| null | null |
\(\boxed{6}\)
|
1. Find the largest natural number consisting of distinct digits such that the product of the digits of this number is 2016.
|
Factorize the number 2016. $2016=2^{5} \cdot 3^{2} \cdot 7$. To make the number as large as possible, it should contain the maximum number of digits. Notice that the number must include the digit 1. Therefore, the number should consist of the digits $1,2,3,6,7,8$.
Grading Criteria. 20 points for the correct answer. 0 points for any other answer.
|
876321
|
Number Theory
|
olympiads
| null | null |
\(\boxed{876321}\)
|
8.2. Find the largest four-digit number in which all digits are different and which is divisible by any of its digits (don't forget to explain why it is the largest).
|
Firstly, the desired number cannot have the form $\overline{987 a}$, because divisibility by the digit 7 would mean that $a$ is 0 or 7. This means the desired number is smaller. Secondly, consider numbers of the form $\overline{986 a}$. Divisibility by the digit 9 would mean that $9+8+6+a=a+23$ is divisible by 9. Therefore, $a=4$. Thus, we get the number 9864. The sum of its digits is 27, so it is divisible by 9, and since the number 864 is divisible by 8, the number itself is divisible by 8. Therefore, it is divisible by 6 and 4.
|
9864
|
Number Theory
|
olympiads
| null | null |
\(\boxed{9864}\)
|
Problem 4.3. All seats at King Arthur's round table are numbered clockwise. The distances between adjacent seats are the same.
One day, King Arthur sat at seat number 10, and Sir Lancelot sat directly opposite him at seat number 29. How many seats are there in total at the round table?
|
Along one side of the table between Arthur and Lancelot are seats numbered $11,12, \ldots, 28$ - a total of exactly 18 seats. Since these two are sitting directly opposite each other, there are also 18 seats on the other side of the table. Therefore, the total number of seats at the table is $18+18+1+1=38$.
|
38
|
Number Theory
|
olympiads
| null | null |
\(\boxed{38}\)
|
Problem 4.7. At the festival of namesakes, 45 Alexanders, 122 Borises, 27 Vasily, and several Gennady arrived. At the beginning of the festival, all of them stood in a row so that no two people with the same name stood next to each other. What is the minimum number of Gennady that could have arrived at the festival?
|
Since there are a total of 122 Boris, and between any two of them stands at least one non-Boris (Alexander/Vasily/Gennady), there are at least 121 non-Boris. Since there are a total of 45 Alexanders and 27 Vasilies, there are at least $121-45-27=49$ Gennadys.
Note that there could have been exactly 49 Gennadys at the festival. Suppose in the line stood 122 Boris. Then 121 gaps between them were filled by other people: the first 45 gaps were filled by one Alexander each, the next 27 by one Vasily each, and the next 49 by one Gennady each. It is easy to see that all conditions of the problem are satisfied.
|
49
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{49}\)
|
Problem 5.1. Dasha calls a natural number special if four different digits are used to write it. For example, the number 3429 is special, while the number 3430 is not special.
What is the smallest special number greater than 3429?
|
Note that all numbers of the form $343 \star$ and $344 \star$ are not special. And the next number after them, 3450, is special.
|
3450
|
Number Theory
|
olympiads
| null | null |
\(\boxed{3450}\)
|
Problem 5.2. At first, the magical island was divided into three counties: in the first county lived only elves, in the second - only dwarves, in the third - only centaurs.
- During the first year, each county where non-elves lived was divided into three counties.
- During the second year, each county where non-dwarves lived was divided into four counties.
- During the third year, each county where non-centaurs lived was divided into six counties.
How many counties were there on the magical island after all these events?
|
Initially, there was 1 county of each kind.
After the first year, there was 1 elven county, 3 dwarf counties, and 3 centaur counties.
After the second year, there were 4 elven counties, 3 dwarf counties, and 12 centaur counties.
After the third year, there were 24 elven counties, 18 dwarf counties, and 12 centaur counties. In total, $24+18+12=54$ counties.
|
54
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{54}\)
|
Problem 5.7. In a magic shop, for 20 silver coins you can buy an invisibility cloak and get 4 gold coins as change. For 15 silver coins you can buy an invisibility cloak and get 1 gold coin as change. How many silver coins will you get as change if you buy an invisibility cloak for 14 gold coins?
|
In the first case, compared to the second, by paying 5 extra silver coins, one can receive 3 extra gold coins in change. Therefore, 5 silver coins are equivalent to 3 gold coins.
In the second case, by paying 15 silver coins (which is equivalent to $3 \cdot 3=9$ gold coins), one can get the cloak and 1 gold coin in change. Therefore, the cloak costs 8 gold coins.
In the third case, by paying 14 gold coins for a cloak worth 8 coins, one would receive 6 gold coins in change, which is equivalent to $5 \cdot 2=10$ silver coins.
|
10
|
Algebra
|
olympiads
| null | null |
\(\boxed{10}\)
|
Problem 5.8. Each of the 33 bogatyrs (Russian epic heroes) either always lies or always tells the truth. It is known that each bogatyr has exactly one favorite weapon: a sword, spear, axe, or bow.
One day, Ded Chernomor asked each bogatyr four questions:
- Is your favorite weapon a sword?
- Is your favorite weapon a spear?
- Is your favorite weapon an axe?
- Is your favorite weapon a bow?
To the first question, 13 bogatyrs answered affirmatively, to the second question - 15 bogatyrs, to the third - 20 bogatyrs, and to the fourth - 27 bogatyrs.
How many bogatyrs always tell the truth?
|
Note that each of the truth-telling heroes answers affirmatively to only one question, while each of the lying heroes answers affirmatively to exactly three questions. Let the number of truth-telling heroes be $x$, and the number of lying heroes be $-(33-x)$. Then the total number of affirmative answers was $13+15+20+27=x+3 \cdot(33-x)$, from which we get $75=99-2 x$ and $x=12$. Note also that the number of truth-telling heroes can be exactly 12. Suppose 8 lying heroes love the sword the most, another 6 lying heroes love the spear, another 1 lying hero loves the axe, another 6 lying heroes love the bow, and another 12 truthful heroes love the bow. It is not difficult to verify that all conditions of the problem are satisfied in this case.
## 6th grade
|
12
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{12}\)
|
Problem 6.1. The set includes 8 weights: 5 identical round, 2 identical triangular, and one rectangular weight weighing 90 grams.
It is known that 1 round and 1 triangular weight balance 3 round weights. Additionally, 4 round weights and 1 triangular weight balance 1 triangular, 1 round, and 1 rectangular weight.
How much does the triangular weight weigh?
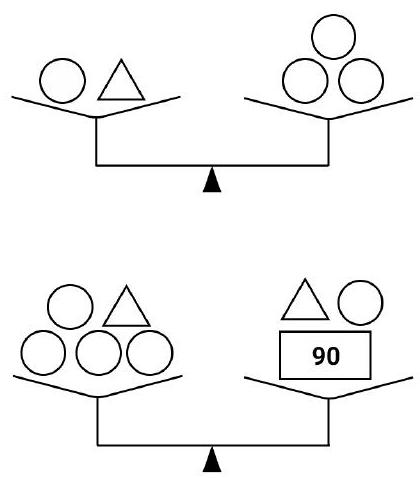
|
From the first weighing, it follows that 1 triangular weight balances 2 round weights.
From the second weighing, it follows that 3 round weights balance 1 rectangular weight, which weighs 90 grams. Therefore, a round weight weighs $90: 3=30$ grams, and a triangular weight weighs $30 \cdot 2=60$ grams.
|
60
|
Algebra
|
olympiads
| null | null |
\(\boxed{60}\)
|
Problem 6.3. In a new math textbook, there are a total of 91 problems. Yura started solving them in the mornings, beginning on September 6.
Every morning, starting from September 7, he solves one fewer problem than the previous morning (until the problems run out).
By the evening of September 8, Yura realized that there were still 46 problems left to solve in the textbook. On which day of September will he finish solving the textbook?
|
In the first 3 days, Yura solved $91-46=45$ problems. Let's say on September 7th, he solved $z$ problems, then on September 6th, he solved $(z+1)$ problems, and on September 8th, he solved $(z-1)$ problems. We get that $45=(z+1)+z+(z-1)=3 z$, from which $z=15$.
Since $91=16+15+14+13+12+11+10$, Yura will solve problems for exactly 7 days, from September 6th to September 12th.
|
12
|
Algebra
|
olympiads
| null | null |
\(\boxed{12}\)
|
Problem 7.2. Petya bought himself shorts for football at the store.
- If he had bought shorts with a T-shirt, the cost of the purchase would have been twice as much.
- If he had bought shorts with cleats, the cost of the purchase would have been five times as much.
- If he had bought shorts with shin guards, the cost of the purchase would have been three times as much.
How many times greater would the cost of the purchase have been if Petya had bought shorts, a T-shirt, cleats, and shin guards?
|
Let the shorts cost $x$. Since the shorts with a T-shirt cost $2x$, the T-shirt also costs $x$. Since the shorts with boots cost $5x$, the boots cost $4x$. Since the shorts with shin guards cost $3x$, the shin guards cost $2x$. Then, if Petya bought shorts, a T-shirt, boots, and shin guards, his purchase would amount to $x+x+4x+2x=8x$, which is 8 times more than $x$.
|
8
|
Algebra
|
olympiads
| null | null |
\(\boxed{8}\)
|
Problem 8.1. In front of a pessimist and an optimist, there are glasses (the glasses are identical). Each of them was given water in their glass such that the pessimist's glass turned out to be $60\%$ empty, while the optimist's glass, on the contrary, was $60\%$ full. It turned out that the amount of water in the pessimist's glass was 46 milliliters less than in the optimist's glass. What is the volume of the glass in milliliters?
|
The pessimist's glass is $40 \%$ full, while the optimist's is $60 \%$ full. The pessimist has $20 \%$ less water than the optimist, which is $\frac{1}{5}$ of the total volume of the glass. Since this difference is 46 milliliters according to the problem, the total volume of the glass is $46 \cdot 5=230$ milliliters.
|
230
|
Algebra
|
olympiads
| null | null |
\(\boxed{230}\)
|
Problem 8.2. On the board, 23 signs are drawn - some pluses and some minuses. If any 10 of them are chosen, there will definitely be at least one plus among them. If any 15 of them are chosen, there will definitely be at least one minus among them. How many pluses are there in total?
|
Since among any 10 signs there is a plus, the number of minuses on the board is no more than 9 (otherwise, we could choose 10 minuses).
Since among any 15 signs there is a minus, the number of pluses on the board is no more than 14 (otherwise, we could choose 15 pluses).
Then the total number of signs on the board is no more than $9+14=23$. Since there are exactly 23 according to the condition, we get that the number of minuses on the board is exactly 9, and the number of pluses is exactly 14.
|
14
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{14}\)
|
Problem 8.3. In the grove, there are 140 chameleons - blue and red. One day, several blue chameleons changed their color to red. As a result, the number of blue chameleons decreased by 5 times, and the number of red chameleons increased by 3 times. How many chameleons changed their color?
|
Let the number of blue chameleons become $x$. Then initially, there were $5 x$ blue chameleons. Accordingly, the number of red chameleons initially was $140-5 x$. Then the number of red chameleons became $3 \cdot(140-5 x)$. Since the total number of chameleons remained the same, we get the equation
$$
x+3 \cdot(140-5 x)=140
$$
Solving it, we find $x=20$. Then the number of chameleons that changed color is $5 x-x=4 x=4 \cdot 20=80$ chameleons.
|
80
|
Algebra
|
olympiads
| null | null |
\(\boxed{80}\)
|
Problem 9.4. In city $\mathrm{N}$, there are exactly three monuments. One day, a group of 42 tourists arrived in this city. Each of them took no more than one photo of each of the three monuments. It turned out that any two tourists together had photos of all three monuments. What is the minimum number of photos that all tourists could have taken in total?
|
Let's number the three monuments. Note that the photo of the first monument is missing from no more than one tourist (otherwise, we could choose two tourists who, in total, have photos of no more than two monuments), so at least $42-1=41$ photos of the first monument were taken. Similarly, at least 41 photos of the second and third monuments were taken. Therefore, a total of at least $41 \cdot 3=123$ photos were taken.
Exactly 123 photos could have been taken, for example, if 1 tourist did not take any photos, and the other 41 each took one photo of each monument. It is clear that in this case, all conditions of the problem are satisfied.
|
123
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{123}\)
|
.2. Given a natural number $n$. Roma wrote down three numbers $n, n+1, n+2$ on the board one after another, without spaces. He obtained a certain sequence of digits, in which there are consecutive digits 6474. Find the smallest possible value of $n$.
|
It is clear that for $n=46$ the condition is satisfied.
Suppose there exists $n<46$. One of the three numbers that Roma has should contain the digit 6, and for $n<46$, it must be in the units place. By a simple enumeration, one can verify that the corresponding values $n=4,5,6,14,15,16,24,25,26,34,35,36,44,45$ do not work.
|
46
|
Number Theory
|
olympiads
| null | null |
\(\boxed{46}\)
|
Problem 11.1. Petya wrote down ten natural numbers in a row as follows: the first two numbers he wrote down arbitrarily, and each subsequent number, starting from the third, was equal to the sum of the two preceding ones. Find the fourth number if the seventh is 42 and the ninth is 110.
|
From the condition, it follows that the eighth number is equal to the difference between the ninth and the seventh, i.e., $110-42=68$. Then the sixth is $68-42=26$, the fifth is $42-26=16$, and the fourth is $26-16=10$.
Remark. In fact, the numbers on the board are the doubled Fibonacci numbers.
|
10
|
Algebra
|
olympiads
| null | null |
\(\boxed{10}\)
|
Problem 11.2. In the store, there are 9 headphones, 13 computer mice, and 5 keyboards. In addition, there are 4 sets of "keyboard and mouse" and 5 sets of "headphones and mouse". In how many ways can you buy three items: headphones, a keyboard, and a mouse? Answer: 646.
|
Let's consider the cases of whether any set was purchased.
- Suppose the set "keyboard and mouse" was purchased, then headphones were added to it. This results in exactly $4 \cdot 9=36$ ways to make the purchase.
- Suppose the set "headphones and mouse" was purchased, then a keyboard was added to it. This results in exactly $5 \cdot 5=25$ ways to make the purchase.
- Suppose no set was purchased, then headphones, mouse, and keyboard were purchased separately. This results in exactly $9 \cdot 13 \cdot 5=585$ ways to make the purchase. In total, there are exactly $36+25+585=646$ desired ways.
|
646
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{646}\)
|
Problem 11.3. The teacher wrote the number 1818 on the board. Vasya noticed that if a multiplication sign is written between the hundreds and tens digits, the value of the resulting expression is a perfect square $\left(18 \times 18=324=18^{2}\right)$. What is the next four-digit number after 1818 that has the same property?
|
Since we need to find the nearest four-digit number, let's try to find it in the form $\overline{18 a b}$. Then the number $18 \cdot \overline{a b}=3^{2} \cdot(2 \cdot \overline{a b})$ must be a perfect square. From this, it follows that $2 \cdot \overline{a b}$ must also be a perfect square. Clearly, $\overline{a b} \in\{19,20,21 \ldots, 31\}$ do not meet this condition, but $\overline{a b}=32$ does. Therefore, the answer to the problem is the number 1832.
Remark. The same answer could have been obtained by proving that $\overline{a b}=2 s^{2}$ for some natural number $s>3$.
|
1832
|
Number Theory
|
olympiads
| null | null |
\(\boxed{1832}\)
|
Problem 11.6. Oleg wrote down several composite natural numbers less than 1500 on the board. It turned out that the greatest common divisor of any two of them is 1. What is the maximum number of numbers that Oleg could have written down?
|
Prime numbers less than $\sqrt{1500}$ will be called small. There are exactly 12 such numbers: $2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37$.
Note that each of Oleg's numbers has a small divisor (otherwise it would be not less than $43^{2} > 1500$), and different numbers have different small divisors (otherwise the GCD of these numbers would be greater than 1). Therefore, the number of Oleg's numbers is no less than the total number of small numbers, i.e., no less than 12.
An example with 12 numbers is easy to construct: these are the numbers $2^{2}, 3^{2}, 5^{2}, 7^{2}, 11^{2}, 13^{2}, 17^{2}, 19^{2}, 23^{2}, 29^{2}, 31^{2}, 37^{2}$.
|
12
|
Number Theory
|
olympiads
| null | null |
\(\boxed{12}\)
|
2. The numbers from 1 to 8 are arranged in a circle. A number is called large if it is greater than its neighbors, and small if it is less than its neighbors. Each number in the arrangement is either large or small. What is the smallest possible sum of the large numbers?
|
Instructions. Adjacent numbers cannot be of the same type, so larger and smaller numbers alternate, and there are four of each. 8 is large. 7 is also large, since a small number must be less than two numbers, and seven is less than only one. 1 and 2 are small. 3 and 4 cannot both be large, as there are only two larger numbers, and they cannot be adjacent in this case. Therefore, the sum of the two other large numbers (besides 7 and 8) is at least 8. And the sum of the large numbers is at least 23. Example: $8,6,7,1,3,2,5,4$.
Criteria. Only the correct answer and example: 2 points.
|
23
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{23}\)
|
Problem 2. There are 22 batteries, 15 of which are charged and 7 are discharged. The camera works with three charged batteries. You can insert any three batteries into it and check if it works. How can you guarantee to turn on the camera in 10 such attempts?
|
Let's number the batteries: $1,2, \ldots, 22$. The first six tests will involve inserting batteries into the camera as follows: $1,2,3 ; 4,5,6 ; \ldots, 16,17,18$. If at least one of these groups turns on the camera, everything is fine. If not, then among the first 18 batteries, there are at least 6 discharged ones, which means that among the last four batteries, there is at most one discharged one. The next four tests will involve trying all combinations of the remaining batteries: $19,20,21 ; 19,20,22 ; 19,21,22 ; 20,21,22$ - and we will definitely find a group of three charged batteries.
- See also problem 1 for 10th grade.
- For an answer without justification - 0 points.
|
10
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{10}\)
|
4. In a joint-stock company, there are 2017 shareholders, and any 1500 of them hold a controlling stake (not less than $50 \%$ of the shares). What is the largest share of shares that one shareholder can have
#
|
# Solution
Let's order the shareholders by the ascending share of their stocks. The 1500th shareholder has no less than $\frac{50}{1500} \%=\frac{1}{30} \%$ of the shares. If the 1500th has less, then the first 1500 shareholders together have less than $50 \%$ of the shares. Therefore, the first 2016 shareholders together have no less than $50 \%+(2016-1500) \frac{1}{30} \%=67.2 \%$ of the shares. The largest share of the 2017th shareholder is $32.8 \%$ of the shares.
## Criteria
A solution that arrives at the correct answer but assumes that each shareholder has no less than $\frac{1}{30} \%$ should be scored 4 points.
If the correct approach is used but one computational error leads to an incorrect answer, score 5 points.
#
|
32.8
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{32.8}\)
|
10.2 About numbers a and b, it is known that the system of equations
$$
\left\{\begin{array}{l}
y^{2}=x^{2}+a x+b \\
x^{2}=y^{2}+a y+b
\end{array}\right.
$$
has no solutions. Find a.
|
Since the system has no solutions, in particular, there are no solutions with $x=y$. When $x=y$, both equations of the system are equivalent to the equation $a x+b=0$. This linear equation has no roots only when its slope coefficient $a$ is zero.
## Criteria:
- Points are not deducted for the absence of an example of a system with $a=0$ that has no solutions.
|
0
|
Algebra
|
olympiads
| null | null |
\(\boxed{0}\)
|
1. Given a finite set of cards. On each of them, either the number 1 or the number -1 is written (exactly one number on each card), and there are 100 more cards with -1 than cards with 1. If for each pair of different cards, the product of the numbers on them is found, and all these products are summed, the result is 1000. How many cards have the number 1?
|
Let the number of cards with 1 be $m$, and the number of cards with -1 be $k$. Then, among all pairs, there are $\frac{m(m-1)}{2}$ pairs of two 1s, $\frac{k(k-1)}{2}$ pairs of two -1s, and $m k$ pairs of 1 and -1. Therefore, the sum in the condition is $\frac{m(m-1)}{2}+\frac{k(k-1)}{2}-m k$, from which we get $m^{2}-2 m k+k^{2}=2000+m+k, (m-k)^{2}=2000+m+k$. According to the condition $k-m=100$, so $m+k=8000$ and $2 m=7900, m=3950$.
Comment: The correct relationship between $k$ and $m$ (in addition to $k-m=100$) has been obtained, but without further progress - 3 points.
|
3950
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{3950}\)
|
1. The bathtub fills with cold water in 6 minutes 40 seconds, with hot water - in 8 minutes. In addition, if the plug is removed from a full bathtub, the water will drain in 13 minutes 20 seconds. How long will it take to fill the bathtub completely, provided that both taps are open, but the bathtub is not plugged?
|
First, we will convert the time in seconds to minutes: 6 minutes 40 seconds will be replaced by $6+2 / 3$, or $20 / 3$, and 13 minutes 20 seconds will be replaced by $13+1 / 3$, or $40 / 3$. Then, in one minute, the cold water will fill $3 / 20$ of the bathtub, the hot water will fill $1 / 8$ of the bathtub, and $3 / 40$ of the bathtub will drain. Therefore, in one minute, the bathtub will fill $3 / 20+1 / 8-3 / 40$, i.e., $1 / 5$ of the bathtub. Thus, the entire bathtub will be filled in 5 minutes.
|
5
|
Algebra
|
olympiads
| null | null |
\(\boxed{5}\)
|
3. In a six-digit number, one digit was crossed out to obtain a five-digit number. The five-digit number was subtracted from the original number, and the result was 654321. Find the original number.
|
Note that the last digit was crossed out, as otherwise the last digit of the number after subtraction would have been zero. Let $y$ be the last digit of the original number, and $x$ be the five-digit number after crossing out. Then the resulting number is $10 x + y - x = 9 x + y = 654321$. Dividing this number by 9 with a remainder (and considering that $y$ does not exceed 9), we get the remainder $y=3$ and the quotient $x=72702$.
|
727023
|
Number Theory
|
olympiads
| null | null |
\(\boxed{727023}\)
|
1. Tourists arrived at the campsite. For lunch, each of them ate half a can of soup, a third of a can of stew, and a quarter of a can of beans. In total, they ate 39 cans of food. How many tourists were there? Answer: 36.
|
Note that 12 tourists ate 6 cans of soup, 4 cans of stew, and 3 cans of beans - that is, a total of 13 cans of food.
39 cans is 3 sets of 13 cans. One set is eaten by 12 people. Therefore, the total number of tourists is 36.
|
36
|
Algebra
|
olympiads
| null | null |
\(\boxed{36}\)
|
2. Six people are standing in a circle, each of whom is either a knight - who always tells the truth, or a liar - who always lies. Each of them said one of two phrases: "There is a liar next to me" or "There is a liar opposite me." What is the minimum number of liars among them? Provide an example and prove that there cannot be fewer liars.
|
Let's number all the people standing clockwise (this way, people with numbers 1 and 4, 2 and 5, 3 and 6 will stand opposite each other).
Zero liars is obviously impossible (then there would be only knights and no one could say any of the phrases).
If there is one liar, let's say his number is 1, then the knight with number 3 has two knight neighbors and a knight standing opposite him. This means he cannot say either of these two phrases.
Example with two liars. Liars have numbers 1 and 2 and say "There is a liar opposite me," which is also said by knights 4 and 5. The remaining knights (3 and 6) say "There is a liar next to me."
|
2
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{2}\)
|
7.2. In Solar City, 6 dwarfs eat donuts daily, 8 dwarfs eat donuts every other day, and the rest do not eat donuts at all. Yesterday, 11 dwarfs ate donuts. How many dwarfs will eat donuts today?
|
Of the 11 dwarfs who ate donuts yesterday, 6 dwarfs eat them daily, so the remaining $11-6=5$ eat them every other day. Therefore, these five will not eat donuts today, while the other $8-5=3$ from those who eat every other day will. So today, these three will eat donuts, as well as the six who always eat donuts. We get the answer $3+6=9$.
Comment: Correct answer without justification -2 points.
|
9
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{9}\)
|
4-8. In a chess club, 90 children attend. During the session, they divided into 30 groups of 3 people, and in each group, everyone played one game with each other. No other games were played. In total, there were 30 games of "boy+boy" and 14 games of "girl+girl". How many "mixed" groups were there, that is, groups where there were both a boy and a girl?
|
There were a total of 90 games, so the number of games "boy+girl" was $90-30-14=46$. In each mixed group, two "boy+girl" games are played, while in non-mixed groups, there are no such games. In total, there were exactly $46 / 2=23$ mixed groups.
## Grade 5
|
23
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{23}\)
|
5-2. In a sports tournament, a team of 10 people participates. The regulations stipulate that 8 players from the team are always on the field, changing from time to time. The duration of the match is 45 minutes, and all 10 participants on the team must play an equal number of minutes. How many minutes will each player be on the field during the game?
|
In total, the players will spend $8 \cdot 45=360$ minutes on the field. This time needs to be divided equally among 10 players, so each will be on the field $360 / 10=36$ minutes.
|
36
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{36}\)
|
5-3. How many two-digit numbers exist where at least one of the digits is smaller than the corresponding digit in the number $35?$
For example, the numbers 17 and 21 are valid, while the numbers 36 and 48 are not.
|
First, let's find the number of two-digit numbers that do not meet the condition. In the units place, any digit from 5 to 9 can stand, and in the tens place, from 3 to 9. The total number of numbers that do not suit us will be exactly $7 \cdot 5=35$. Now we can count the number of two-digit numbers that meet the condition: we need to subtract the number of unsuitable numbers from their total number, which is 90: $90-35=55$.
|
55
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{55}\)
|
5-8. In the "Young Photographer" club, 300 children attend. During the class, they divided into 100 groups of 3 people, and in each group, each person took one photo of the other two in their group. No one took any other photos. In total, there were 100 photos of "boy+boy" and 56 photos of "girl+girl". How many "mixed" groups were there, that is, groups that had both a boy and a girl?
|
There were a total of 300 photos, so the number of photos of "boy+girl" was $300-100-56=144$. Each mixed group provides two photos of "boy+girl", while non-mixed groups do not provide such photos. Therefore, there were exactly $144 / 2=72$ mixed groups.
## 6th grade
|
72
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{72}\)
|
6-1. The physical education teacher lined up the class so that everyone was facing him. To the right of Kolya, there are 12 people, to the left of Sasha - 20 people, and to the right of him - 8 people. How many people are standing to the left of Kolya?
|
Since there are 20 people to the left of Sasha and 8 people to the right of him, there are a total of 28 people in the row, not counting Sasha. Therefore, including Sasha, there are 29 people in the class. Then, to the left of Kolya, there are $29-12-1=16$ people (first subtracting the 12 people who are to the right of Kolya, and then Kolya himself).
|
16
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{16}\)
|
6-5. Grandma baked 21 batches of dumplings, with $N$ dumplings in each batch, $N>70$. Then she laid out all the dumplings on several trays, with 70 dumplings on each tray. What is the smallest possible value of $N$?
|
The total number of baked buns is $21 \cdot N$. This number must be divisible by 70 to be able to distribute them into several trays of 70 each. $70=2 \cdot 5 \cdot 7$, and 21 is already divisible by 7. Therefore, $N$ must be divisible by 10, and the smallest such $N$ is 80.
|
80
|
Number Theory
|
olympiads
| null | null |
\(\boxed{80}\)
|
6-7. In a confectionery store, the saleswoman laid out 91 candies of several varieties in a row on the counter. It turned out that between any two candies of the same variety, there was an even number of candies. What is the smallest number of varieties there could have been?
|
We will prove that there could not have been three or more candies of the same type. Indeed, let candies of the same type $A, B$, and $C$ lie in that exact order. Suppose there are $2x$ candies between $A$ and $B$, and $2y$ candies between $B$ and $C$, then there are $2x + 2y + 1$ candies between $A$ and $C$, which is an odd number of candies, contradicting the condition.
Since there are no more than 2 candies of each type, there must be at least 46 types. Let's provide an example where there could be 46 types. For instance, the candies can be arranged in pairs: two of the first type, two of the second type, and so on for 45 pairs, with one more candy of the 46th type at the end. There are many other examples.
|
46
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{46}\)
|
7-1. Petya has stickers. If he gives 5 stickers to each of his friends, he will have 8 stickers left. If he wants to give 6 stickers to each of his friends, he will be short of 11 stickers. How many friends does Petya have?
|
I. Suppose Petya gave 5 stickers to each of his friends. Next, he wants to give each friend one more sticker. For this, he needs to spend $8+11=19$ stickers, and he gives one sticker to each friend, so he has 19 friends.
Solution II. Let Petya have $x$ friends. Then $5 x+8=6 x-11$, from which $x=19$.
|
19
|
Algebra
|
olympiads
| null | null |
\(\boxed{19}\)
|
7-6. In an ornithological park, there are several species of birds, a total of 2021 individuals. The birds sat in a row, and it turned out that between any two birds of the same species, there was an even number of birds. What is the smallest number of bird species that could have been there?
|
Estimation. We will prove that there could not have been three or more birds of the same species. Indeed, suppose birds of the same species $A, B$, and $C$ sit in that exact order. Let there be $2x$ birds between $A$ and $B$, and $2y$ birds between $B$ and $C$, then there are $2x + 2y + 1$ birds between $A$ and $C$, which is an odd number of birds, contradicting the condition. Since there are no more than 2 birds of each species, there must be at least 1011 species.
Example. We will provide an example where 1011 species could have been present. For instance, the birds could sit in pairs: two of the first species, two of the second species, and so on up to the 1010th species, with one more bird of the 1011th species at the end. There are many other examples.
|
1011
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{1011}\)
|
9-3. Arina wrote down all the numbers from 71 to 81 in a row without spaces, forming a large number 717273...81. Sofia started appending the next numbers to it (i.e., she first appended 82, then 83, ...). She stopped when the large number became divisible by 12. The last number she appended was $N$. What is $N$?
|
A number is divisible by 12 if and only if it is divisible by 3 and by 4. For a number to be divisible by 4, the number formed by its last two digits must also be divisible by 4. Therefore, the last number that Sofia writes must be divisible by 4.
The nearest number that is divisible by 4 is 84, but the number 71727374...84 has a sum of digits equal to 158, which means it is not divisible by 3. The next number that is divisible by 4 is 88. The sum of the digits of the number 71727374...88 is 216, which means the entire number is divisible by 3.
|
88
|
Number Theory
|
olympiads
| null | null |
\(\boxed{88}\)
|
10-1. There are several bowls on the table, each containing several grapes. Different bowls may contain different numbers of grapes. If 12 bowls are each added 8 more grapes, the average number of grapes in all the bowls will increase by 6. How many bowls are on the table
|
Let the number of bowls be $n$. The total number of berries increased by $12 \cdot 8=96$. Since the average number of berries increased by 6, the total number of berries should have increased by $6n$. Therefore, $6n=96$, from which we find $n=16$.
|
16
|
Algebra
|
olympiads
| null | null |
\(\boxed{16}\)
|
10-4. Initially, a natural number was displayed on the calculator screen. Each time, Olya added a natural number to the current number \( n \) on the calculator screen, which \( n \) did not divide. For example, if the screen showed the number 10, Olya could add 7 to get 17.
Olya repeated this operation five times, and the number 200 appeared on the screen. What is the largest initial number for which this could have happened?
|
Estimation. Note that Olya increased the number on the screen by at least 2 each time, because any number is divisible by 1. If Olya added two five times, the initial number would have been 190, and it would not have been possible to add two to it. Therefore, Olya must have added a number greater than two at least once. Consequently, she increased the number by at least 11 in total, from which $n \leqslant 189$.
Estimation. For $n=189$, this is possible: $200=189+2+2+2+2+3$.
|
189
|
Number Theory
|
olympiads
| null | null |
\(\boxed{189}\)
|
11-4. At first, a natural number was displayed on the calculator screen. Each time, Tanya added to the current number \( n \) on the screen a natural number that \( n \) did not divide. For example, if the screen showed the number 10, Tanya could add 7 to get 17.
Tanya repeated this operation five times, and the number 100 appeared on the screen. What is the largest initial number for which this could have happened?
|
Estimation. Note that Tanya increased the number on the screen by at least 2 each time, because any number is divisible by 1. If Tanya added two five times, the initial number would have been 90, and it would not have been possible to add two to it. Therefore, Tanya must have added a number greater than two at least once. Consequently, she increased the number by at least 11 in total, from which $n \leqslant 89$.
Estimation. For $n=89$, this is possible: $100=89+2+2+2+2+3$.
|
89
|
Number Theory
|
olympiads
| null | null |
\(\boxed{89}\)
|
11-6. Petya uses all possible ways to place the signs + and - in the expression $1 * 2 * 3 * 4 * 5 * 6$ in the places of the asterisks. For each arrangement of the signs, he calculates the resulting value and writes it on the board. On the board, some numbers may appear multiple times. Petya adds up all the numbers on the board. What is the sum obtained by Petya?
|
Note that each of the digits $2,3,4,5,6$ will contribute zero to Petya's sum: each will equally often appear with a + sign and with a - sign. The digit 1 will appear in all sums with a + sign as many times as there are addends in total. Since each of the asterisks can take two values, there will be $2^{5}=32$ addends. Therefore, Petya's sum is 32.
|
32
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{32}\)
|
1. Variant 1.
When multiplying two two-digit numbers, a four-digit number $A$ is obtained, where the first digit matches the second, and the second-to-last digit matches the last. Find the smallest $A$, given that $A$ is divisible by 51.
|
Notice that $A=\overline{x x y y}=x \cdot 11 \cdot 100+y \cdot 11=11 \cdot(100 x+y)$. Since 51 and 11 are coprime, then $100 x+y$ is divisible by 51. The minimum $x=1$, so $y=2$ (the only number from 100 to 109 divisible by 51 is 102).
|
1122
|
Number Theory
|
olympiads
| null | null |
\(\boxed{1122}\)
|
2. Variant 1.
Find the number of four-digit numbers for which the last three digits form an increasing arithmetic progression (numbers cannot start with zero).
|
The difference of the progression cannot be greater than 4.
For $d=1$ - there are eight suitable progressions of digits: from 012 to 789.
For $d=2$ - six: from 024 to 579.
For $d=3$ - four: from 036 to 369.
For $d=4$ - two: 048 and 159.
In total, $8+6+4+2=20$ options for the last three digits. By choosing the first digit in nine ways for each of them, we get the answer $20 \cdot 9=180$.
|
180
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{180}\)
|
3. Variant 1.
Find the ratio $\frac{16 b^{2}}{a c}$, given that one of the roots of the equation $a x^{2}+b x+c=0$ is 4 times the other.
|
By Vieta's theorem, $-\frac{b}{a}=x_{1}+x_{2}=5 x_{2}$ and $\frac{c}{a}=x_{1} \cdot x_{2}=4 x_{2}^{2}$. Express $x_{2}=-\frac{b}{5 a}$ from the first equation and substitute it into the second: $\frac{c}{a}=\frac{4 b^{2}}{25 a^{2}}$. Then find $\frac{b^{2}}{a c}=\frac{25}{4}$.
|
100
|
Algebra
|
olympiads
| null | null |
\(\boxed{100}\)
|
8.2. Vasya replaced identical digits in two numbers with identical letters, and different digits with different letters. It turned out that the number ZARAZA is divisible by 4, and ALMAZ is divisible by 28. Find the last two digits of the sum ZARAZA + ALMAZ.
|
From the condition, it follows that the numbers ZARAZA and ALMAZ are divisible by 4. By the property of divisibility by 4, the numbers ZA and AZ are also multiples of 4. In particular, it follows from this that both digits 3 and A are even. But a number divisible by 4, in which the second-to-last digit is even, must end in a digit that is a multiple of 4. Therefore, both digits 3 and A are multiples of 4. Since they are non-zero (they start the numbers ZARAZA and ALMAZ), one of them is 4, and the other is 8.
The specified sum ends with the same 2 digits as $3 \mathrm{~A}+\mathrm{A} 3=48+84=132$, that is, with 32.
|
32
|
Number Theory
|
olympiads
| null | null |
\(\boxed{32}\)
|
# 6.1. Condition:
Petya thought of a natural number and wrote down the sums of each pair of its digits on the board. After that, he erased some of the sums, and the numbers $2,0,2,2$ remained on the board. What is the smallest number Petya could have thought of?
|
## Solution.
Since among the sums there is a 0, the number must contain at least two digits 0. If the number has only three digits, there will be three pairwise sums, while the condition states there are at least four. Therefore, the number must have at least four digits. A sum of 2 can be obtained either as $1+1$ or as $2+0$. If the number contains the digit 2, then it will have four digits, three of which are $-2,0,0$, which means the number cannot be less than 2000. At the same time, 2000 meets the condition. If 2 is obtained as $1+1$, then at least four digits $-1,1,0,0$ are required. With these, it is impossible to get pairwise sums of $2,0,2$, 2, which means there must be at least 5 digits, i.e., the number will definitely be greater than 2000.
|
2000
|
Number Theory
|
olympiads
| null | null |
\(\boxed{2000}\)
|
5. Misha has a $7 \times 7$ square of paper, all cells of which are white. Misha wants to color $N$ cells black. What is the smallest $N$ for which Misha can color the cells so that after coloring, no completely white rectangle with at least ten cells can be cut out from the square?
|
Divide the $7 \times 7$ square into 5 rectangles: four $3 \times 4$ rectangles (each corner of such a rectangle coincides with one of the corners of the $7 \times 7$ square) and a $1 \times 1$ square. If only three cells are colored, there will be a white rectangle consisting of 12 cells. Example for 4 cells: color $b 4, d 2, d 6, f 4$ in chess notation.
Criteria. Only the answer - 0 points. Correct example for 4 cells - 3 points. Proof that 3 black cells are not enough - 4 points. Points for parts of this problem are summed.
|
4
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{4}\)
|
2. Find the value of the fraction
$$
\frac{2 \cdot 2020}{1+\frac{1}{1+2}+\frac{1}{1+2+3}+\ldots+\frac{1}{1+2+3+\ldots+2020}}
$$
|
Let's denote the denominator of the fraction by $q$. By repeatedly applying the formula for the sum of an arithmetic progression, we get that
$$
q=\frac{2}{1 \cdot 2}+\frac{2}{2 \cdot 3}+\frac{2}{3 \cdot 4}+\ldots+\frac{2}{2020 \cdot 2021}
$$
Now, using the identity $\frac{1}{k(k+1)}=\frac{1}{k}-\frac{1}{k+1}$, we get
$$
q=\frac{2}{1}-\frac{2}{2}+\frac{2}{2}-\frac{2}{3}+\frac{2}{3}-\frac{2}{4}+\frac{2}{4}-\ldots+\frac{2}{2020}-\frac{2}{2021}=\frac{2 \cdot 2020}{2021}
$$
Substituting this expression into the original fraction and simplifying it, we get the answer: 2021.
|
2021
|
Algebra
|
olympiads
| null | null |
\(\boxed{2021}\)
|
3. How to measure 8 liters of water when you are near a river and have two buckets with a capacity of 10 liters and 6 liters? (8 liters of water should end up in one bucket).
|
Let's write the sequence of filling the buckets in the form of a table:
| | Bucket with a capacity of 10 liters | Bucket with a capacity of 6 liters | Comment |
| :--- | :--- | :--- | :--- |
| Initially | 0 liters | 0 liters | |
| Step 1 | 10 liters | 0 liters | Filled the first bucket from the river |
| Step 2 | 4 liters | 6 liters | Poured from the first bucket into the second until it was full |
| Step 3 | 4 liters | 0 liters | Poured the second bucket back into the river |
| Step 4 | 0 liters | 4 liters | Poured from the first bucket into the second bucket |
| Step 5 | 10 liters | 4 liters | Filled the first bucket from the river again |
| Step 6 | 8 liters | 6 liters | Poured from the first bucket into the second until it was full |
|
8
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{8}\)
|
4. Snow White entered a room where there were 30 chairs around a round table. Some of the chairs were occupied by dwarfs. It turned out that Snow White could not sit down without having someone next to her. What is the minimum number of dwarfs that could have been at the table? (Explain how the dwarfs should have been seated and why, if there were fewer dwarfs, there would be a chair with no one sitting next to it).
|
If there were three consecutive empty chairs at the table in some place, Snow White could sit down in such a way that no one would sit next to her. Therefore, in any set of three consecutive chairs, at least one must be occupied by a dwarf. Since there are 30 chairs in total, there cannot be fewer than 10 dwarfs. We will show that it is possible to seat 10 dwarfs in such a way that the condition of the problem is satisfied: we will seat the dwarfs every three chairs: on the first chair, on the fourth chair, on the seventh chair, and so on. Then the condition of the problem will be met.
|
10
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{10}\)
|
3. We will call a number palindromic if it reads the same from left to right as it does from right to left. For example, the number 12321 is palindromic.
a) Write any palindromic five-digit number that is divisible by 5.
b) How many five-digit palindromic numbers are there that are divisible by 5?
a) Solution. Any palindromic number ending in 5. For example, 51715.
b) Answer. 100.
|
A number that is divisible by 5 must end in 5 or 0. A palindromic number cannot end in 0, as then it would have to start with 0. Therefore, the first and last digits are 5. The second and third digits can be anything - from the combination 00 to the combination 99 - a total of 100 options. Since the fourth digit repeats the second, there will be 100 different numbers in total.
|
100
|
Number Theory
|
olympiads
| null | null |
\(\boxed{100}\)
|
3. We will call a number palindromic if it reads the same from left to right as it does from right to left. For example, the number 12321 is palindromic. How many five-digit palindromic numbers are there that are divisible by 5?
|
A number that is divisible by 5 must end in 5 or 0. A mirrored number cannot end in 0, as then it would have to start with 0. Therefore, the first and last digits are 5. The second and third digits can be anything from the combination 00 to the combination 99 - a total of 100 options. Since the fourth digit repeats the second, there will be a total of 100 different numbers.
|
100
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{100}\)
|
2. (7 points) It is known that $a^{2}+b=b^{2}+c=c^{2}+a$. What values can the expression $a\left(a^{2}-b^{2}\right)+b\left(b^{2}-c^{2}\right)+c\left(c^{2}-a^{2}\right)$ take?
## Answer: 0.
|
Note that the equality $a^{2}+b=b^{2}+c$ can be written as: $a^{2}-b^{2}=c-b$. Similarly, we have $b^{2}-c^{2}=a-c, c^{2}-a^{2}=b-a$. Substituting these equalities into the desired expressions, we get that
$$
a\left(a^{2}-b^{2}\right)+b\left(b^{2}-c^{2}\right)+c\left(c^{2}-a^{2}\right)=a(c-b)+b(a-c)+c(b-a)=0
$$
Criteria. Any correct solution: 7 points.
Only the correct answer is provided: 0 points.
|
0
|
Algebra
|
olympiads
| null | null |
\(\boxed{0}\)
|
5. (7 points) Lёsha did not hesitate to calculate the sum
$$
9+99+999+\ldots+\underbrace{9 \ldots 9}_{2017}
$$
and wrote it on the board. How many times is the digit 1 written in the final result?
|
Transform the expression:
$$
\begin{aligned}
9+99+999+\ldots+\underbrace{9 \ldots 9}_{2017} & =(10-1)+(100-1)+\ldots+\left(10^{2017}-1\right)= \\
& =\underbrace{1 \ldots 10}_{2017}-2017=\underbrace{1 \ldots 1}_{2013} 09093 .
\end{aligned}
$$
Criteria. Any correct solution: 7 points.
It is shown that the original sum is equal to $\underbrace{1 \ldots 10}_{2017}-2017$, but further solution is missing or contains an arithmetic error: 5 points. Only the correct answer is provided: 1 point.
|
2013
|
Number Theory
|
olympiads
| null | null |
\(\boxed{2013}\)
|
1. Variant 1.
Petya has four cards with digits $1,2,3,4$. Each digit appears exactly once. How many natural numbers greater than 2222 can Petya make from these cards?
|
Let's find out how many different numbers can be formed from these cards: the first digit can be chosen in 4 ways, the second can be appended in 3 ways, the third in 2 ways, and the last one is uniquely determined. That is, a total of 24 different numbers can be obtained (it is also possible to verify this explicitly by listing all suitable numbers). Let's find out how many of the listed numbers will not suit us. These are all numbers starting with 1, there are 6 of them. And 2 more numbers: 2134, 2143, because if the number starts with 2, the second digit can only be 1. Then the suitable numbers are $24-6-2=16$.
|
16
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{16}\)
|
2. Variant 1.
Nine integers from 1 to 5 are written on the board. It is known that seven of them are not less than 2, six are greater than 2, three are not less than 4, and one is not less than 5. Find the sum of all the numbers.
|
A number not less than 5 is 5. There is exactly one number 5. Three numbers are not less than 4, so exactly two numbers are equal to 4. Six numbers are greater than 2, meaning all of them are not less than 3. Therefore, exactly three numbers are equal to 3. Seven numbers are not less than 2, so one number is equal to 2. In total, there are 9 numbers, hence two numbers are equal to 1. The sum of all numbers is $1+1+2+3+3+3+4+4+5=26$.
|
26
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{26}\)
|
# 3. Option 1.
Café "Buratino" operates 6 days a week with a day off on Mondays. Kolya said that from April 1 to April 20, the café was open for 17 days, and from April 10 to April 30, it was open for 18 days. It is known that he made a mistake once. What was the date of the last Tuesday in April?
|
Since there are exactly 21 days from April 10 to April 30, each day of the week occurred exactly 3 times during this period. Therefore, this statement cannot be false. This means the first statement is false, and there were only 2 Mondays from April 1 to April 20 (there could not have been four, as at least 22 days would be needed for that). This could only happen if April 1 was a Tuesday. Therefore, the last Tuesday in April was the 29th.
|
29
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{29}\)
|
5. Variant 1.
In the addition example, where the numbers were written on cards, two cards were swapped, resulting in the incorrect expression: $37541+43839=80280$. Find the error and write down the correct sum.
|
Let's start checking the example from right to left. There are no errors in the units and tens place, but an error appears in the hundreds place. This means that one of the digits in this place $-2, 8$ or $5-$ is transposed.
Let's consider the following cases:
|
80380
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{80380}\)
|
# 6. Option 1.
Nезнайка named four numbers, and Ponchik wrote down all their pairwise sums on six cards. Then he lost one card, and the numbers left on the remaining cards were $270, 360, 390, 500, 620$. What number did Ponchik write on the lost card?
|
Let the original numbers be $a \leq b \leq c \leq d$. Suppose the card with the maximum sum is lost. Then this sum is $c+d$. Therefore, $a+b=270$ and $a+b+c+d>270+620=890$. On the other hand, the sum of all numbers on the cards is $3a+3b+2c+2d=270+360+390+500+620=2140$. We get that $2140>1780+2c+2d$, hence $c+d<180$. This is a contradiction. Similarly, we can prove that the card with the smallest numbers was not lost. Therefore, the sum of all numbers on the cards is $270+620=890$. All pairwise sums can be divided into the following groups: 1) $a+b, c+d$, 2) $a+c, b+d$, 3) $a+d, b+c$. The sum of the numbers in each group is 890. This is only possible if the lost card has the number $890-360=530$, since 620 and 270, 390 and 500 form pairs.
|
530
|
Algebra
|
olympiads
| null | null |
\(\boxed{530}\)
|
7. Variant 1.
101 natural numbers are written in a circle. It is known that among any 3 consecutive numbers, there is at least one even number. What is the smallest number of even numbers that can be among the written numbers?
|
Consider any 3 consecutive numbers. Among them, there is an even number. Fix this number and its neighbor, and divide the remaining 99 into 33 sets of 3 consecutive numbers. In each such set, there is at least one even number. Thus, the total number of even numbers is no less than $1+33=34$. Such a situation is possible. Number the numbers in a circle. The even numbers can be those with numbers $1,4,7, \ldots, 100$
|
34
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{34}\)
|
1. In 2022, knights and liars lined up, with the extreme left and right being liars. Everyone except the extremes made the statement: “There are 42 times more liars to the right of me than to the left.” Provide an example of a row where there is exactly one knight.
|
Note that $2021=43 * 47$, so if we place the knight as the forty-eighth from the left, there will be 47 liars to his left, and to his right there will be 2021-47=42*47 liars.
Grading criteria: Correct example - 7 points, if "left" and "right" are switched, do not deduct points. In other cases - 0 points.
|
48
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{48}\)
|
# Task 9.1
All three-digit numbers are written in a row: $100101102 \ldots 998$ 999. How many times in this row does a zero follow a two?
## Number of points 7 Answer: 19
#
|
# Solution
Since a three-digit number cannot start with zero, the two followed by a zero cannot be in the units place of any three-digit number in the sequence. Let's assume the two is in the tens place of a three-digit number. Then the zero following it is in the units place of the same number, i.e., the number ends in 20. There are 9 such numbers: 120, 220, ..., 920. Finally, if the two followed by a zero is in the hundreds place, then the corresponding three-digit number starts with 20. There are 10 such numbers: 200, 201, ..., 209. Therefore, the zero will follow the two 19 times in total.
|
19
|
Number Theory
|
olympiads
| null | null |
\(\boxed{19}\)
|
6.1. In the numerical example АБВ $+9=$ ГДЕ, the letters А, Б, В, Г, Д, and Е represent six different digits. What digit is represented by the letter Д?
|
In the addition, the second digit of the first addend АБВ has changed (Д instead of Б). This could only happen if 1 was carried over from the units place to the tens place during the addition. However, the first digit also changed (Г instead of А). This means that 1 was also carried over from the tens place to the hundreds place during the addition. This is only possible if Б $+1=10$. Therefore, $Б=9$, and then $Д=0$.
Note: The puzzle has solutions, for example, $194+9=203$.
Comment: The score is not reduced if the correct answer is given, it is stated that $Б=9$, $Д=0$, but detailed explanations are not provided.
|
0
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{0}\)
|
6.5. In the room, there are 10 people - liars and knights (liars always lie, and knights always tell the truth). The first said: "In this room, there is at least 1 liar." The second said: "In this room, there are at least 2 liars." The third said: "In this room, there are at least 3 liars." And so on,
up to the tenth, who said: "In this room, everyone is a liar." How many liars could there be among these 10 people?
|
Let there be $k$ liars in the room. Then the first $k$ people told the truth (and thus were knights), while the remaining $(10-k)$ lied (and were liars). Therefore, $k=10-k$, from which $k=5$.
Comment: The answer is obtained by considering an example -3 points.
|
5
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{5}\)
|
6. In a checkers tournament, students from 10th and 11th grades participated. Each player played against every other player once. A player received 2 points for a win, 1 point for a draw, and 0 points for a loss. There were 10 times more 11th graders than 10th graders, and together they scored 4.5 times more points than all the 10th graders. How many points did the most successful 10th grader score?
|
Let $a$ be the number of tenth graders who participated in the tournament, earning $b$ points. Then, $10a$ eleventh graders played, earning $4.5b$ points. In each match, 2 points are played for, and a total of $11a$ players play $\frac{11 a(11 a-1)}{2}$ matches. Therefore, from the condition of the problem, we have the equation $11 a(11 a-1)=5.5 b$, from which it follows that $b=2 a(11 a-1)$.
|
20
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{20}\)
|
Problem 9.2. The least common multiple of four pairwise distinct numbers is 165. What is the maximum value that the sum of these numbers can take?
|
Since 165 is the least common multiple of four numbers, these numbers are divisors of 165. To maximize the sum of these numbers, it is sufficient to take the four largest divisors of 165. If one of them is the number 165 itself, then the LCM will definitely be equal to it.
Then the maximum sum will be
$$
165+\frac{165}{3}+\frac{165}{5}+\frac{165}{11}=165+55+33+15=268
$$
|
268
|
Number Theory
|
olympiads
| null | null |
\(\boxed{268}\)
|
Problem 9.3. The teacher wrote a fraction on the board, where the numerator and the denominator are natural numbers. Misha added 30 to the numerator of the given fraction and wrote the resulting fraction in his notebook, while Lesha subtracted 6 from the denominator of the fraction written on the board and also wrote the resulting fraction in his notebook. The fractions recorded by the boys turned out to be equal to the same number. What is this number?
|
Let $\frac{a}{b}$ be the original fraction. Then Misha wrote down the fraction $\frac{a+30}{b}$ in his notebook, and Lёsha wrote down $-\frac{a}{b-6}$.
Let's write the equation
$$
\frac{a+30}{b}=\frac{a}{b-6}
$$
Transforming it, we get
$$
\begin{gathered}
(a+30)(b-6)=a b \\
a b+30 b-6 a-180=a b ; \\
30 b=6 a+180 \\
\frac{a+30}{b}=5
\end{gathered}
$$
This is the value of the fraction obtained by Misha. It should also have been obtained by Lёsha.
|
5
|
Algebra
|
olympiads
| null | null |
\(\boxed{5}\)
|
Problem 9.5. On the board, the graph of the function $y=x^{2}+a x+b$ is drawn. Yulia drew two lines parallel to the $O x$ axis on the same drawing. The first line intersects the graph at points $A$ and $B$, and the second line intersects the graph at points $C$ and $D$. Find the distance between the lines if it is known that $A B=5, C D=11$.
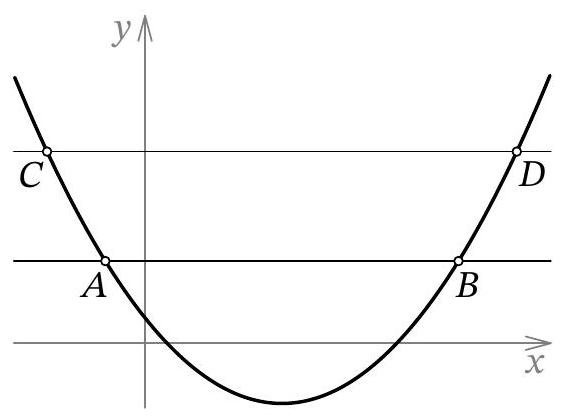
|
Let the first line have the equation $y=s$, and the second line have the equation $y=t$. Then the distance between the lines is $(t-s)$.
The length of segment $A B$ is equal to the absolute value of the difference of the roots of the equation $x^{2}+a x+b=s$. We can express the difference of the roots using the formula for solving the quadratic equation $x^{2}+a x+(b-s)=0$:
$$
\frac{-a+\sqrt{a^{2}-4(b-s)}}{2}-\frac{-a-\sqrt{a^{2}-4(b-s)}}{2}=\sqrt{a^{2}-4(b-s)}=5
$$
from which we derive
$$
a^{2}-4(b-s)=25
$$
Similarly, we obtain
$$
a^{2}-4(b-t)=121
$$
Subtract the first equation from the second and we get
$$
121-25=\left(a^{2}-4(b-t)\right)-\left(a^{2}-4(b-s)\right)=4(t-s)
$$
We have $4(t-s)=96$, that is, $t-s=24$.
|
24
|
Algebra
|
olympiads
| null | null |
\(\boxed{24}\)
|
1.1 A courtyard table tennis tournament among 15 players is held according to certain rules. In each round, two players are randomly selected to compete against each other. After the round, the loser receives a black card. The player who receives two black cards is eliminated from the competition. The last remaining player is declared the champion. In table tennis, there are no ties. How many rounds were there in the courtyard tournament if the champion lost exactly once?
|
In each match, there is always exactly one loser. Since 14 players were eliminated, there were a total of $14 \cdot 2+1=29$ losses.
|
29
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{29}\)
|
4.1 Seven pirates were dividing five identical treasure chests. They agreed that five of them would take one chest each, while the others would receive a fair compensation equal to the value of a chest. Each of the recipients of a chest paid 10000 piastres into a common fund, after which the money was distributed among the remaining pirates. What was the value of one chest?
|
Two pirates received 50000 piastres, so each share amounted to 25000. Since the chests were divided fairly, the total amount of treasure was 25000 for each of the seven, totaling 175000. Then 175000 is the value of five chests, meaning each chest was valued at 35000 piastres.
|
35000
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{35000}\)
|
4. It is known that the numbers EGGPLANT and FROG are divisible by 3. What is the remainder when the number CLAN is divided by 3? (Letters represent digits, the same letters represent the same digits, different letters represent different digits).
Answer: 0
|
By the divisibility rule for 3, the sums B+A+K+L+A+Z+A+N and Z+A+B+A are divisible by 3, and therefore the difference of these sums $K+N+A+H$ is also divisible by 3, which by the rule means that the number KLAN is divisible by 3, hence the remainder is 0.
Criteria. Only the answer - 0 points
|
0
|
Number Theory
|
olympiads
| null | null |
\(\boxed{0}\)
|
8.1. Usually, we write the date in the format of day, month, and year (for example, 17.12.2021). In the USA, however, it is customary to write the month number, day number, and year in sequence (for example, 12.17.2021). How many days in a year cannot be determined unequivocally by its writing?
|
Obviously, these are the days where the date can be the number of the month, that is, it takes values from 1 to 12. There are such days $12 \times 12=144$. But the days where the number matches the month number are unambiguous. There are 12 such days. Therefore, the number of days sought is $144-12=132$.
|
132
|
Other
|
olympiads
| null | null |
\(\boxed{132}\)
|
8.3. Find the value of the expression $\frac{a^{2}}{b c}+\frac{b^{2}}{a c}+\frac{c^{2}}{a b}$, if $a+b+c=0$.
|
$(a+b+c)^{3}=a^{3}+b^{3}+c^{3}+(a+b+c)(3 a b+3 b c+3 c a)-3 a b c$. Using the condition $a+b+c=0$, we get: $a^{3}+b^{3}+c^{3}=3 a b c$. Then $\frac{a^{2}}{b c}+\frac{b^{2}}{a c}+\frac{c^{2}}{a b}=\frac{a^{3}+b^{3}+c^{3}}{a b c}=\frac{3 a b c}{a b c}=3$
|
3
|
Algebra
|
olympiads
| null | null |
\(\boxed{3}\)
|
2. What is the minimum number of factors that need to be crossed out from the number 99! (99! is the product of all numbers from 1 to 99) so that the product of the remaining factors ends in 2?
|
From the number 99! all factors that are multiples of 5 must be removed, otherwise the product will end in 0. There are 19 such factors in total.
The product of the remaining factors ends in 6. Indeed, the product $1 \cdot 2 \cdot 3 \cdot 4 \cdot 6 \cdot 7 \cdot 8 \cdot 9$ ends in 6, and similar products in each subsequent decade also end in 6. Therefore, it is sufficient to remove one more factor, for example, 8. After this, the product of the remaining factors will end in 2.
|
20
|
Number Theory
|
olympiads
| null | null |
\(\boxed{20}\)
|
9.1. It is known that $a^{2}+b=b^{2}+c=c^{2}+a$. What values can the expression
$$
a\left(a^{2}-b^{2}\right)+b\left(b^{2}-c^{2}\right)+c\left(c^{2}-a^{2}\right) ?
$$
take?
|
From the condition, it follows that $a^{2}-b^{2}=c-b$, $b^{2}-c^{2}=a-c$, and $c^{2}-a^{2}=b-a$. Therefore, $a\left(a^{2}-b^{2}\right)+b\left(b^{2}-c^{2}\right)+c\left(c^{2}-a^{2}\right)=a(c-b)+b(a-c)+c(b-a)=0$.
## Grading Criteria:
+ a complete and justified solution is provided
the correct answer is obtained by considering specific examples
- only the answer is provided
- the problem is not solved or is solved incorrectly
|
0
|
Algebra
|
olympiads
| null | null |
\(\boxed{0}\)
|
11.1. Anya left the house, and after some time Vanya left from the same place and soon caught up with Anya. If Vanya had walked twice as fast, he would have caught up with Anya three times faster. How many times faster would Vanya have caught up with Anya (compared to the actual time) if, in addition, Anya walked twice as slow
|
Let Ane's speed be $v$, and Vanya's speed be $V$. The distance Ane has walked is proportional to $v$, while Vanya catches up with her at a speed of $u=V-v$. When Vanya doubles his speed, this difference triples, i.e., $u+V=2V-v=3u$. From this, we get $V=2u=2v$. If Vanya's speed doubles and Ane's speed is halved, the new difference in speeds will be $3.5v$, which is 7 times the new speed of Masha. Therefore, Vanya will catch up to her 7 times faster.
|
7
|
Algebra
|
olympiads
| null | null |
\(\boxed{7}\)
|
11.2. In a box, there are white and blue balls, with the number of white balls being 8 times the number of blue balls. It is known that if you pull out 100 balls, there will definitely be at least one blue ball among them. How many balls are there in the box?
|
Since the number of white balls in the box is 8 times the number of blue balls, the total number of balls in the box is divisible by 9. Since 100 balls are drawn from it, the smallest possible number of balls in the box $n=108$, of which 12 are blue and 96 are white. Since there are fewer than a hundred white balls, there will be blue balls in any set of a hundred balls. If $n>108$, then $n \geq 117$ (since $n$ is divisible by 9). In this case, the number of white balls will be greater than or equal to 104, and there will be sets of a hundred balls that do not contain any blue balls.
|
108
|
Number Theory
|
olympiads
| null | null |
\(\boxed{108}\)
|
4. For what least natural $\mathrm{k}$ does the quadratic trinomial
$$
y=k x^{2}-p x+q \text { with natural coefficients } p \text{ and } q \text{ have two }
$$
distinct positive roots less than 1?
|
First, let's estimate the coefficient $\mathrm{k}_{\text{from below. Let }} 0k^{2} x_{1}\left(1-x_{1}\right) x_{2}\left(1-x_{2}\right) \geq 1 \Rightarrow k>4 \text{. Thus, we have obtained the }$
$$
$$
lower bound. To show the accuracy of the estimate, it is sufficient to construct an example with $k=5: y=5 x^{2}-5 x+1$.
Recommendations for checking: Constructing only an example, without an estimate - 3 points;
Obtaining only the estimate (without an example) - 4 points.
## Recommendations for checking
Constructing only an example, without an estimate - 3 points;
Obtaining only the estimate (without an example) - 4 points.
|
5
|
Algebra
|
olympiads
| null | null |
\(\boxed{5}\)
|
Problem 4.2. Petya has 25 coins, each with a denomination of $1, 2, 5$, or 10 rubles. Among these coins, 19 are not two-ruble coins, 20 are not ten-ruble coins, and 16 are not one-ruble coins. How many five-ruble coins does Petya have?
|
Since among Petya's coins, 19 are not two-ruble coins, Petya has a total of 6 two-ruble coins. Similarly, it follows that Petya has 5 ten-ruble coins and 9 one-ruble coins.
Thus, Petya has $25-6-5-9=5$ five-ruble coins.
|
5
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{5}\)
|
Problem 5.3. By September 1st, Vlad bought himself several ballpoint and gel pens. He noticed that if all the pens he bought were gel pens, he would have paid 4 times more than he actually did. And if all the pens were ballpoint pens, the purchase would have cost him 2 times less than the actual price. How many times more expensive is a gel pen compared to a ballpoint pen?
|
If all the pens were gel pens, their price would be 4 times the actual price, which in turn is 2 times more than if all the pens were ballpoint pens. Therefore, gel pens cost $4 \cdot 2=8$ times more than ballpoint pens. Consequently, one gel pen is 8 times more expensive than one ballpoint pen.
|
8
|
Algebra
|
olympiads
| null | null |
\(\boxed{8}\)
|
Problem 5.6. Vanya received three sets of candies as a New Year's gift. In the sets, there are three types of candies: lollipops, chocolate, and jelly. The total number of lollipops in all three sets is equal to the total number of chocolate candies in all three sets, as well as the total number of jelly candies in all three sets. In the first set, there are an equal number of chocolate and jelly candies, and 7 more lollipops. In the second set, there are an equal number of lollipops and chocolate candies, and 15 fewer jelly candies. How many candies are in the third set, if it is known that there are no lollipops there?
|
There are more lollipops than jelly candies in the first set by 7, and in the second set by 15. Since the total number of each type of candy is the same in all sets, and there are 0 lollipops in the third set, there must be $7+15=22$ jelly candies in the third set.
Similarly, there are more lollipops than chocolate candies in the first set by 7, and in the second set by 0. Since the total number of each type of candy is the same in all sets, and there are 0 lollipops in the third set, there must be 7 chocolate candies in the third set.
Therefore, the total number of candies in the third set is $22+7+0=29$.
|
29
|
Algebra
|
olympiads
| null | null |
\(\boxed{29}\)
|
Problem 6.3. Three merchants: Foma, Yerema, and Julius met in Novgorod. If Foma gives Yerema 70 gold coins, then Yerema and Julius will have the same amount of money. If Foma gives Yerema 40 gold coins, then Foma and Julius will have the same amount of money. How many gold coins should Foma give Yerema so that they both have the same amount of money?
|
From the first condition, it follows that Yuliy has 70 more coins than Yeremy. From the second condition, it follows that Foma has 40 more coins than Yuliy. Therefore, Foma has $40+70=110$ more coins than Yeremy. For them to have an equal amount of money, Foma must give Yeremy half of this difference, which is $\frac{110}{2}=55$ coins.
|
55
|
Algebra
|
olympiads
| null | null |
\(\boxed{55}\)
|
Problem 6.4. In a coastal village, 7 people go fishing every day, 8 people go fishing every other day, 3 people go fishing every three days, and the rest do not fish at all. Yesterday, 12 people went fishing, and today, 10 people are fishing. How many people will go fishing tomorrow?
|
Let's calculate how many times in total they fished yesterday and today. 7 people who fish every day fished 2 times each, i.e., a total of 14 times. 8 people who fish every other day fished exactly 1 time each, i.e., a total of 8 times. Therefore, these 15 people fished a total of $14+8=22$ times over the past two days.
According to the problem, they fished $12+10=22$ times in total over the past two days. Therefore, the fishermen who fish every three days were not present yesterday and today, and they will all come to fish tomorrow. Additionally, 7 people who fish every day will come tomorrow, and $12-7=5$ fishermen who fish every other day will also come. Thus, a total of $3+7+5=15$ people will come to fish tomorrow.
|
15
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{15}\)
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.