problem
stringlengths 17
4.31k
| solution_hint
stringlengths 49
6.77k
| answer
stringlengths 1
44
⌀ | problem_type
stringclasses 8
values | source
stringclasses 2
values | level
stringclasses 3
values | type
stringclasses 7
values | solution
stringlengths 13
56
|
|---|---|---|---|---|---|---|---|
Problem 6.6. Four girls and eight boys came to take a class photo. The children approach the photographer in pairs and take a joint photo. Among what minimum number of
photos will there definitely be either a photo of two boys, or a photo of two girls, or two photos of the same children?
|
Suppose at some point there is neither a photo of two boys, nor a photo of two girls, nor two photos of the same children. Then, on each photo, there is a boy and a girl, and on different photos, there are different pairs. However, the total number of possible pairs consisting of a boy and a girl is $4 \cdot 8=32$, and each of these pairs can be captured in no more than one photo. Therefore, among any 33 photos, there must be either a photo of people of the same gender, or two photos of the same pair of people.
At the same time, 32 photos may not be enough: they can capture different pairs consisting of a boy and a girl.
|
33
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{33}\)
|
Problem 7.1. Petya wrote 20 natural numbers 1, 2, .., 20 on the board. Vasya first erased all even numbers, and then erased all numbers that give a remainder of 4 when divided by 5. How many numbers are left on the board
|
After erasing all even numbers, the following remain on the board:
$$
\begin{array}{llllllllll}
1 & 3 & 5 & 7 & 9 & 11 & 13 & 15 & 17 & 19 .
\end{array}
$$
Among them, exactly two give a remainder of 4 when divided by 5 - these are 9 and 19. After erasing these as well, 8 numbers remain on the board.
|
8
|
Number Theory
|
olympiads
| null | null |
\(\boxed{8}\)
|
Problem 7.3. The pages in a book are numbered as follows: the first sheet is two pages (with numbers 1 and 2), the second sheet is the next two pages (with numbers 3 and 4), and so on. The hooligan Petya tore out several consecutive sheets from the book: the first torn page has the number 185, and the number of the last torn page consists of the same digits but in a different order. How many sheets did Petya tear out?
|
Since any leaf ends with a page number that is an even number, the number of the last torn-out page is either 158 or 518. But 158 does not work, since 158 < 185. Therefore, the last page ends with the number 518. Now let's calculate the number of torn-out pages. Among the pages from 1 to 518, the pages from 1 to 184 were not torn out. Therefore, 518 - 184 = 334 pages were torn out. There are half as many leaves, which is 334 / 2 = 167.
|
167
|
Number Theory
|
olympiads
| null | null |
\(\boxed{167}\)
|
Problem 7.6. The distance between cities A and B is an integer number of kilometers. Along the road between the cities, there is a signpost every kilometer: on one side is the distance to city A, and on the other side is the distance to city B. Slava walked from city A to city B. During his journey, Slava calculated the GCD of the numbers on each signpost. It turned out that among the calculated GCDs, only the numbers 1, 3, and 13 appeared. What is the distance between the cities?
|
Suppose we are standing next to a sign with numbers $x$ and $y$ written on it. If $\text{GCD}(x, y) = d$, then $(x + y) \vdots d$, i.e., the distance between the cities is divisible by all the calculated GCDs.
Now suppose the distance between the cities (let's call it $S$) is divisible by some natural number $d$. Then at a distance of $d$ kilometers from city A, the numbers on the sign are $d$ and $S - d$, and the GCD of these numbers is exactly $d$.
From all this, we conclude that 1, 3, and 13 are the complete list of divisors of the distance between the cities (excluding the distance itself). Therefore, the distance is 39 kilometers.
|
39
|
Number Theory
|
olympiads
| null | null |
\(\boxed{39}\)
|
Problem 7.7. In the election for class president, Petya and Vasya competed. Over three hours, 27 students in the class voted for one of the two candidates. In the first two hours, Petya received 9 more votes than Vasya. In the last two hours, Vasya received 9 more votes than Petya. In the end, Petya won. By what maximum number of votes could he have won?
|
In the last two hours, at least 9 people voted for Vasya. This means that in the end, he received at least 9 votes. Then Petya received no more than $27-9=18$ votes. Therefore, his lead in votes does not exceed $18-9=9$.
Now let's provide an example of how a lead of 9 votes could be achieved. Suppose that in the first hour, 18 people voted for Petya, and in the second hour, 9 people voted for Vasya. It is easy to see that all the conditions of the problem are satisfied, and Petya won with a lead of 9 votes.
|
9
|
Algebra
|
olympiads
| null | null |
\(\boxed{9}\)
|
Problem 8.2. The numbers from 1 to 9 were placed in the cells of a $3 \times 3$ table such that the sum of the numbers on one diagonal is 7, and on the other - 21. What is the sum of the numbers in the five shaded cells?
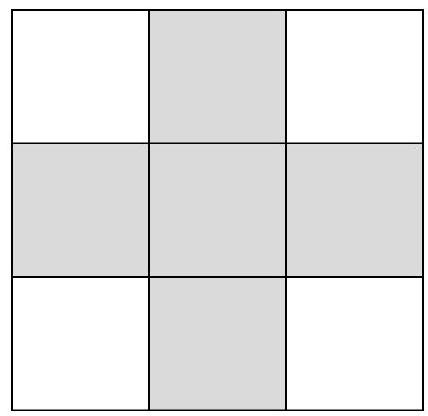
|
Note that 7 can be represented uniquely as the sum of numbers from 1 to 9 - this is $1+2+4=7$.
Let's look at the other diagonal with a sum of 21. The largest possible value of the sum in it is $9+8+4=21$ (since the number in the central cell is no more than 4). Therefore, it must contain the numbers $9,8,4$.
Thus, the number 4 is in the central cell, and the numbers 1, 2, 8, and 9 are at the corners. Now it is not difficult to find the sum of the numbers in the shaded cells: $3+4+5+6+7=25$.
|
25
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{25}\)
|
Problem 8.3. Four children were walking along an alley and decided to count the number of firs planted along it.
- Anya said: "There are a total of 15 firs along the alley."
- Borya said: "The number of firs is divisible by 11."
- Vера said: "There are definitely fewer than 25 firs."
- Gena said: "I am sure that their number is divisible by 22."
One boy and one girl were right, while the other two were wrong. How many firs grow along the alley?
|
Let $N-$ be the number of elms along the alley.
Suppose Genya told the truth, and $N$ is divisible by 22. But then $N$ is also divisible by 11, i.e., Borya also told the truth. But according to the problem, one of the boys was wrong. Therefore, Genya must have been wrong, but Borya was right. So, $N$ is divisible by 11 but not by 22.
Since 15 is not divisible by 11, Anya must have been wrong. Then Vera told the truth, and $N<25$. But there is exactly one number less than 25 that is divisible by 11 and not by 22, which is 11. It is easy to verify that $N=11$ satisfies all the conditions of the problem.
|
11
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{11}\)
|
Problem 8.5. At the ball, ladies and gentlemen arrived - in total less than 50 people. During the first dance, only a quarter of the ladies were not invited to dance, and 2/7 of the total number of gentlemen did not invite anyone. How many people came to the ball? (For the dance, a certain gentleman invites a certain lady.)
|
Let the number of ladies be $n$, and the number of gentlemen be $m$. We will count the number of pairs who danced. On one hand, it is $\frac{3}{4} n$, and on the other hand, $\frac{5}{7} m$. By equating, we find the ratio
$$
\frac{n}{m}=\frac{20}{21}
$$
Since the fraction on the right side is irreducible, we get that $n=20 k$ and $m=21 k$ for some natural number $k$. It remains to note that the total number of people $20 k +$ $21 k=41 k$ is less than 50, so only $k=1$ fits, and the total number of people at the ball is $20+21=41$.
|
41
|
Number Theory
|
olympiads
| null | null |
\(\boxed{41}\)
|
Problem 8.7. For three real numbers $p, q$, and $r$, it is known that
$$
p+q+r=5, \quad \frac{1}{p+q}+\frac{1}{q+r}+\frac{1}{p+r}=9
$$
What is the value of the expression
$$
\frac{r}{p+q}+\frac{p}{q+r}+\frac{q}{p+r} ?
$$
|
Multiply the two given equalities, we get
$$
5 \cdot 9=\frac{p+q+r}{p+q}+\frac{p+q+r}{q+r}+\frac{p+q+r}{p+r}=\left(1+\frac{r}{p+q}\right)+\left(1+\frac{p}{q+r}\right)+\left(1+\frac{q}{p+r}\right)
$$
Subtract 3 from both sides of the equation, we get
$$
\frac{r}{p+q}+\frac{p}{q+r}+\frac{q}{p+r}=42
$$
|
42
|
Algebra
|
olympiads
| null | null |
\(\boxed{42}\)
|
Problem 9.3. To 30 palm trees in different parts of an uninhabited island, a sign is nailed.
- On 15 of them, it is written: "Exactly under 15 signs, treasure is buried."
- On 8 of them, it is written: "Exactly under 8 signs, treasure is buried."
- On 4 of them, it is written: "Exactly under 4 signs, treasure is buried."
- On 3 of them, it is written: "Exactly under 3 signs, treasure is buried."
It is known that only the signs under which there is no treasure are true.
Under what minimum number of signs can the treasure be buried?
|
Suppose the treasure is not buried under at least 16 plaques. Then there are two plaques with different inscriptions under which there is no treasure. According to the condition, the inscriptions on both should be true, but they contradict each other. Contradiction.
Therefore, the treasure is not buried under more than 15 plaques. Thus, there are at least 15 plaques under which there is treasure. It is not difficult to come up with a suitable example: let the treasures be buried only under plaques with one of the following three phrases.
- "The treasure is buried under exactly 8 plaques."
- "The treasure is buried under exactly 4 plaques."
- "The treasure is buried under exactly 3 plaques."
|
15
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{15}\)
|
Problem 9.5. Buratino has many coins of 5 and 6 soldi, more than 10 of each type. Coming to the store and buying a book for $N$ soldi, he realized that he could not pay for it without receiving change. What is the greatest value that the natural number $N$ can take if it is no more than 50?
|
It is easy to check that with $N=19$ change is necessary.
Notice that numbers from 20 to 24 do not meet the condition, as they can be paid for without change: $N=20=4 \cdot 5, 21=3 \cdot 5+6, 22=2 \cdot 5+2 \cdot 6, 23=5+3 \cdot 6, 24=4 \cdot 6$.
It is clear that then numbers from 25 to 50 also do not meet the condition, as each of them is the sum of one or more terms equal to 5, as well as a number from 20 to 24, which is the sum of terms, each equal to 5 and 6.
|
19
|
Number Theory
|
olympiads
| null | null |
\(\boxed{19}\)
|
Problem 10.3. Yura has $n$ cards, on which numbers from 1 to $n$ are written. After losing one of them, the sum of the numbers on the remaining cards turned out to be 101. What number is written on the lost card?
|
Suppose that $n \leqslant 13$. Then $1+2+\ldots+n=\frac{n(n+1)}{2} \leqslant 91101$, a contradiction.
Therefore, $n=14$, and the missing number is $1+2+\ldots+14-101=105-101=4$.
|
4
|
Number Theory
|
olympiads
| null | null |
\(\boxed{4}\)
|
Problem 10.7. Oleg has four cards, on each of which natural numbers are written on both sides (a total of 8 numbers are written). He considers all possible quadruples of numbers, where the first number is written on the first card, the second on the second, the third on the third, and the fourth on the fourth. Then, for each quadruple, he writes down the product of the numbers in his notebook. What is the sum of the eight numbers on the cards if the sum of the sixteen numbers in Oleg's notebook is $330 ?$
|
Let the numbers on one card be $a$ and $b$, on another card - $c$ and $d$, on the third card - $e$ and $f$, and on the fourth card - $g$ and $h$. According to the problem, the sum of 16 terms of the form $a c e g + a c e h + \ldots + b d f h$ equals 330. Note that this sum is also obtained by expanding all the brackets in the expression $(a+b)(c+d)(e+f)(g+h)$.
Therefore, $(a+b)(c+d)(e+f)(g+h)=330=2 \cdot 3 \cdot 5 \cdot 11$. Since all numbers are natural, each bracket is greater than 1. Hence, the brackets are equal to the numbers $2, 3, 5$, and 11 in some order. Then their sum is $a+b+c+d+e+f+g+h=2+3+5+11=21$.
|
21
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{21}\)
|
.7. For what least natural $x$ is the expression
$$
\sqrt{29+\sqrt{x}}+\sqrt{29-\sqrt{x}}
$$
an integer?
|
If we square the given expression, we get $58+2 \sqrt{29^{2}-x}$. If the initial expression was an integer, then this number is a perfect square. We need to find the smallest $x$, i.e., we need to make this expression the largest possible perfect square. Notice that $58+2 \sqrt{29^{2}-x}<58+2 \sqrt{29^{2}}=116$. The largest square less than 116 is 100. Solving the equation $58+2 \sqrt{29^{2}-x}=100$, we get $x=400$. It is not difficult to verify that when $x=400$, the original expression is indeed an integer.
|
400
|
Algebra
|
olympiads
| null | null |
\(\boxed{400}\)
|
Problem 8.6.1. Even natural numbers $a$ and $b$ are such that $\operatorname{GCD}(a, b) + \operatorname{LCM}(a, b) = 2^{23}$. How many different values can $\operatorname{LCM}(a, b)$ take?
|
Note that LCM $(a, b) \vdots$ GCD $(a, b)$, therefore
$$
2^{23}=\text { GCD }(a, b)+\text { LCM }(a, b) \vdots \text { GCD }(a, b) .
$$
From this, it follows that GCD $(a, b)$ is a natural divisor of the number $2^{23}$.
At the same time, GCD $(a, b) \neq 1$ (since $a$ and $b-$ are even numbers), and GCD $(a, b) \neq 2^{23}$ (since GCD $\left.(a, b)=2^{23}-\operatorname{LCM}(a, b)<2^{23}\right)$. Thus, GCD $(a, b)$ takes one of the values $2,2^{2}, 2^{3}, \ldots, 2^{22}$.
Note that all these values are possible: to make GCD $(a, b)$ equal to $2^{k}$ for $1 \leqslant k \leqslant 22$, it is sufficient to choose $a=2^{k}$ and $b=2^{23}-2^{k}$. In this case, $b \vdots a$, so GCD $(a, b)=a$ and LCM $(a, b)=b$, that is, GCD $(a, b)+$ LCM $(a, b)=a+b=2^{23}$.
|
22
|
Number Theory
|
olympiads
| null | null |
\(\boxed{22}\)
|
Problem 8.8.1. Different positive numbers $a, b, c$ are such that
$$
\left\{\begin{array}{l}
a^{2}+b c=115 \\
b^{2}+a c=127 \\
c^{2}+a b=115
\end{array}\right.
$$
Find $a+b+c$.
|
Subtract the third equation from the first and transform:
$$
\begin{gathered}
\left(a^{2}+b c\right)-\left(c^{2}+a b\right)=0 \\
a^{2}-c^{2}+b c-a b=0 \\
(a-c)(a+c)+b(c-a)=0 \\
(a-c)(a+c-b)=0
\end{gathered}
$$
By the condition $a \neq c$, therefore $b=a+c$. Now add the first two equations:
$$
\begin{gathered}
\left(a^{2}+b c\right)+\left(b^{2}+a c\right)=115+127 \\
\left(a^{2}+b c\right)+\left(b^{2}+a c\right)=242
\end{gathered}
$$
Substitute $b=a+c$ into the resulting equation:
$$
\begin{aligned}
242 & =a^{2}+b c+b^{2}+a c=a^{2}+(a+c) c+(a+c)^{2}+a c= \\
& =a^{2}+a c+c^{2}+(a+c)^{2}+a c=2(a+c)^{2}
\end{aligned}
$$
from which $(a+c)^{2}=121$. Since the numbers $a$ and $c$ are positive and $b=a+c$, we get that $a+c=11$ and $a+b+c=22$.
|
22
|
Algebra
|
olympiads
| null | null |
\(\boxed{22}\)
|
1. Variant 1. Given two natural numbers. One number was increased by 3, and the other was decreased by 3. As a result, their product increased by 600. By how much will the product decrease if the opposite is done: the first number is decreased by 3, and the second is increased by 3?
|
Let these numbers be $a$ and $b$. Then, according to the condition, $(a-3)(b+3)-ab=600$. Expanding the brackets: $ab+3a-3b-9-ab=600$, so $a-b=203$. We need to find the difference $ab-(a+3)(b-3)=$ $ab-ab+3a-3b+9=3(a-b)+9=3 \cdot 203+9=618$.
|
618
|
Algebra
|
olympiads
| null | null |
\(\boxed{618}\)
|
2. Variant 1. At the intersection of perpendicular roads, a highway from Moscow to Kazan and a road from Vladimir to Ryazan intersect. Dima and Tolya set out with constant speeds from Moscow to Kazan and from Vladimir to Ryazan, respectively. When Dima passed the intersection, Tolya had 900 meters left to reach it. When Tolya passed the intersection, Dima was 600 meters away from it. How many meters will be between the boys when Tolya has traveled 900 meters from the moment he crossed the intersection?
|
When Tolya has traveled 900 meters, Dima will have traveled 600 meters, so at the moment when Tolya is 900 meters from the intersection, Dima will be 1200 meters from the intersection. According to the Pythagorean theorem, the distance between the boys is 1500 meters.
|
1500
|
Algebra
|
olympiads
| null | null |
\(\boxed{1500}\)
|
3. Variant 1. Petya and Masha take candies from a box in turns. Masha took one candy, then Petya took 2 candies, Masha - 3 candies, Petya - 4 candies, and so on. When the number of candies in the box became less than needed for the next turn, all the remaining candies went to the one whose turn it was to take candies. How many candies did Petya get if Masha got 101 candies
|
Since $1+3+5+7+9+11+13+15+17+19=100101$, then Masha got the last candy. Then Petya took for himself $2+4+6+8+10+12+14+16+18+20=2(1+2+3+4+5+6+7+8+9+10)=110$ candies.
|
110
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{110}\)
|
# 5. Option 1.
It is known that the equations $x^{2}+(2 a-5) x+a^{2}+1=0$ and $x^{3}+(2 a-5) x^{2}+\left(a^{2}+1\right) x+a^{2}-4=0$ have common roots. Find the sum of these roots.
|
The left side of the second equation is obtained from the left side of the first equation by multiplying by $x$ and adding the expression $a^{2}-4$. Therefore, $a^{2}-4=0$, from which $a=2$ or $a=-2$. If $a=2$, then the first equation has no roots. Therefore, $a=-2$, and then we get that the first equation is of the form: $x^{2}-9 x+5=0$. By Vieta's theorem, we find that the desired sum is 9.
|
9
|
Algebra
|
olympiads
| null | null |
\(\boxed{9}\)
|
6. Variant 1. Grisha thought of such a set of 10 different natural numbers that their arithmetic mean is 16. What is the maximum possible value of the largest of the numbers he thought of?
|
The sum of the given numbers is $10 \cdot 16=160$. Since all the numbers are distinct, the sum of the 9 smallest of them is no less than $1+2+\cdots+9=45$. Therefore, the largest number cannot be greater than $160-45=115$. This is possible: $(1+2+\cdots+9+115): 10=16$.
|
115
|
Number Theory
|
olympiads
| null | null |
\(\boxed{115}\)
|
7. Variant 1. Roma decided to create his own multiplication table. The rows correspond to the numbers 12, $13,14, \ldots, 60$, and the columns - to the numbers $15,16,17, \ldots, 40$. In the cells of the table, he wrote the products of the pairs of numbers from the row and column. How many of these products will be even numbers?
|
Note that the product of two numbers is odd if and only if both factors are odd, and even in all other cases. In total, the table contains 49$\cdot$26 products. Note that among the numbers from 12 to 60, there are 24 odd numbers, and among the numbers from 15 to 40, there are 13 odd numbers. Therefore, there will be $24 \cdot 13$ odd products in the table. The remaining $49 \cdot 26-24 \cdot 13=962$ will be even.
|
962
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{962}\)
|
1. Fishermen caught several carp and pike. Each one caught as many carp as all the others caught pike. How many fishermen were there if the total number of carp caught was 10 times the number of pike?
## Answer: 11.
#
|
# Solution:
Let the total number of fishermen be $n$. Denote the total number of carp caught as $K$. This sum is equal to the sum of carp caught by each, i.e., it is equal to the sum of pike caught by all fishermen, counted $(n-1)$ times.
Thus, we have the equation: $K=10 \frac{K}{n-1}$.
From this - the answer
|
11
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{11}\)
|
3. On Eeyore's Birthday, Winnie-the-Pooh, Piglet, and Owl came to visit. When Owl left, the average age in this company decreased by 2 years, and when Piglet left, the average age decreased by another 1 year. How many years older is Owl than Piglet?
Answer: Owl is 6 years older than Piglet.
|
Let the average age of those who remained after Piglet be x, and Piglet's age be y. Then $2x + y = 3(x + 1)$, which means $y = x + 3$. Let Owl's age be K. Then $3(x + 1) + K = 4(x + 3)$, which means $K = x + 9$. Therefore, Owl is older than Piglet by $(x + 9) - (x + 3) = 6$ years.
Criteria. If the solution is incorrect - 0 points.
If the reasoning is correct but there is a computational error - 3 points. If the solution is correct - 7 points.
|
6
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{6}\)
|
1. Five consecutive natural numbers were written on the board, and then one number was erased. It turned out that the sum of the remaining four numbers is 2015. Find the smallest of these four numbers.
|
If the smallest number is K, then the sum of all numbers is not less than $\mathrm{K}+(\mathrm{K}+1)+(\mathrm{K}+2)+ (\mathrm{K}+3)=4 \mathrm{~K}+6$ and not more than $\mathrm{K}+(\mathrm{K}+2)+(\mathrm{K}+3)+(\mathrm{K}+4)=4 \mathrm{~K}+9$. Therefore, $4 \mathrm{~K}+6 \leq 2015 \leq 4 \mathrm{~K}+9$, from which $\mathrm{K}=502$.
|
502
|
Number Theory
|
olympiads
| null | null |
\(\boxed{502}\)
|
3. What can the value of the expression $p^{4}-3 p^{3}-5 p^{2}+16 p+2015$ be if $p$ is a root of the equation $x^{3}-5 x+1=0$?
Answer: 2018
|
$\mathrm{p}^{4}-3 \mathrm{p}^{3}-5 \mathrm{p}^{2}+16 \mathrm{p}+2015=\left(\mathrm{p}^{3}-5 \mathrm{p}+1\right)(\mathrm{p}-3)+2018$. Since $\mathrm{p}$ is a root of the polynomial in the first parenthesis, the entire expression equals 2018.
|
2018
|
Algebra
|
olympiads
| null | null |
\(\boxed{2018}\)
|
Problem 9.1. Find the largest five-digit number, the product of whose digits is 120.
|
The largest single-digit divisor of the number $120-8$, so the desired number definitely starts with this digit. The product of all the remaining digits is 15.
The largest single-digit divisor of the number $15-5$, so the digit in the thousands place will be this digit. The product of the last three digits is three 3, so the largest number will end with 311.
|
85311
|
Number Theory
|
olympiads
| null | null |
\(\boxed{85311}\)
|
Problem 9.2. During the first half of the year, lazy Pasha forced himself to solve math problems. Every day he solved no more than 10 problems, and if on any day he solved more than 7 problems, then for the next two days he solved no more than 5 problems per day. What is the maximum number of problems Pasha could solve in 7 consecutive days?
|
Suppose Pasha solved at least 8 tasks (but no more than 10) in one of the first five days, then in the next two days he solved no more than 5 tasks per day. Thus, in these three days, he solved no more than $20(10+5+5)$ tasks. If he solved 7 tasks each day, it would be more.
It turns out that in the first five days, Pasha solved no more than 35 tasks. It remains to note that in the last two days, he solved no more than 17 tasks (since he could not exceed the limit of 7 tasks on both days), and he could solve 17 tasks (7 tasks on the sixth day and 10 tasks on the seventh day).
|
52
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{52}\)
|
Problem 10.3. Anton wrote three natural numbers $a, b$, and $c$ on the board. Ira drew three rectangles $a \times b, a \times c$, and $b \times c$ on the board. It turned out that the difference in the areas of one pair of rectangles is 1, and the difference in the areas of another pair of rectangles is 49. What can $a+b+c$ be? List all possible options.
|
Without loss of generality, we assume that $1=ac-ab=a(c-b)$, then $a=1$, $c=b+1$. Thus, the numbers written on the board were $1, b, b+1$.
Notice that either $b(b+1)-b \cdot 1=49$, or $b(b+1)-(b+1) \cdot 1=49$.
In the first case, we get $b^{2}=49, b=7$, and $a+b+c=1+b+(b+1)=16$.
In the second case, we get $b^{2}=50$. Such natural $b$ does not exist.
|
16
|
Number Theory
|
olympiads
| null | null |
\(\boxed{16}\)
|
Problem 11.2. Vera has a set of weights of different masses, each weighing an integer number of grams. It is known that the lightest weight in the set weighs 71 times less than all the other weights combined. It is also known that the two lightest weights in the set together weigh 34 times less than all the other weights combined. What is the smallest number of grams the lightest weight can weigh?
|
All weights in the solution are expressed in grams.
Let the lightest weight be $m$, then the other weights are $71 m$, and the total weight is $72 \mathrm{~m}$. Let also the two lightest weights together weigh $n$, then the other weights weigh $34 n$, and the total weight is $35 n$, which is divisible by 35. Therefore, $72 m$ is divisible by 35, i.e., $m$ is divisible by 35, since 72 and 35 are coprime.
Thus, $m \geqslant 35$. Now let's provide an example of a possible set of weights where $m=35$. For the set of weights with different weights $35,37,48,2400$, all conditions are met: $35 \cdot 71=$ $2485=37+48+2400,(35+37) \cdot 34=2448=48+2400$.
|
35
|
Number Theory
|
olympiads
| null | null |
\(\boxed{35}\)
|
5. Option 1.
Petya is the oldest child in the family. He has two sisters, Anya and Katya, and a brother Vasya. Petya calculated that Anya and Katya together are 19 years old, and Anya and Vasya together are 14 years old. Determine how old Katya is, if it is known that the two youngest children together are 7 years old.
|
Pete cannot be among the two younger children, and among the remaining children, the unconsidered pair is Katya and Vasya, so together they are 7 years old. If you add Katya's age to Anya's age, it will be 5 years more than if you add Vasya's age to Anya's age, so Anya is 5 years older than Vasya. But together, Katya and Vasya are 7 years old. Therefore, Katya is 6 years old, and Vasya is 1 year old.
|
6
|
Algebra
|
olympiads
| null | null |
\(\boxed{6}\)
|
9.5. To a natural number $N$, the largest divisor of $N$ less than $N$ was added, and the result was a power of ten. Find all such $N$. (N. Agakhanov)
|
Let $m$ be the greatest divisor of the number $N$, less than $N$. Then $n=mp$, where $p$ is the smallest prime divisor of the number $N$. We have $N+m=10^{k}$, that is, $m(p+1)=10^{k}$. The number on the right side is not divisible by 3, so $p>2$. From this, it follows that $N$ is an odd number, and therefore $m$ is also odd. Thus, since $10^{k}$ is divisible by $m$, we get $m=5^{s}$. If $m=1$, then $N=p=10^{k}-1$, which is impossible since $10^{k}-1$ is divisible by 9, and thus is not a prime. Therefore, $s \geqslant 1$, the number $N$ is divisible by 5, and hence $p \leqslant 5$. If $p=3$, we get the equation $4 \cdot 5^{s}=10^{k}$, from which $k=2, m=25$, and $N=75$. If $p=5$, then $p+1=6$, and the number $10^{k}$ is divisible by 3, which is impossible.
|
75
|
Number Theory
|
olympiads
| null | null |
\(\boxed{75}\)
|
10.5. To a natural number $N$, the largest divisor of $N$ less than $N$ was added, and the result was a power of ten. Find all such $N$.
(N. Agakhanov)
|
Let $m$ be the greatest divisor of the number $N$, less than $N$. Then $n=m p$, where $p$ is the smallest prime divisor of the number $N$. We have $N+m=10^{k}$, that is, $m(p+1)=10^{k}$. The number on the right side is not divisible by 3, so $p>2$. From this, it follows that $N$ is an odd number, and therefore $m$ is also odd. Since $10^{k}$ is divisible by $m$, we get $m=5^{s}$. If $m=1$, then $N=p=10^{k}-1$, which is impossible since $10^{k}-1$ is divisible by 9, and thus is not a prime. Therefore, $s \geqslant 1$, the number $N$ is divisible by 5, and hence $p \leqslant 5$. If $p=3$, we get the equation $4 \cdot 5^{s}=10^{k}$, from which $k=2, m=25$, and $N=75$. If $p=5$, then $p+1=6$, and the number $10^{k}$ is divisible by 3, which is impossible.
|
75
|
Number Theory
|
olympiads
| null | null |
\(\boxed{75}\)
|
1. First, we will calculate the number of ways to choose three points out of the 60 available. The first point can be chosen in 60 ways, the second in 59 ways, and the third in 58 ways; as a result, we get $205320=60 \cdot 59 \cdot 58$ options. Since the selections of vertices ABC, ACB, CBA, CAB, BAC, and BCA all give the same triangle, the number of ways to choose three points without considering the order of selection is 205320:6=34220. We will not be satisfied with the sets of three points that lie on the same straight line. There are exactly 30 such sets. Therefore, there are $34220-30=34190$ ways to construct the given triangles.
|
Recommendations for evaluating solutions: to determine the number of triplets of points, one can use the combination formula $C_{60}^{3}=\frac{60!}{3!57!}=34220$.
|
34190
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{34190}\)
|
2. (7 points) In Sun City, they exchange a honey cake for 6 pretzels, and for 9 pretzels, they give 4 doughnuts. How many doughnuts will they give for 3 honey cakes? Explain your answer.
|
If for one cookie you get 6 pretzels, then for 3 cookies you will get $3 \times 6=18$ pretzels. 18 pretzels is 2 times 9 pretzels. Therefore, for them, you will get 2 times 4 gingerbread cookies, i.e., 8 gingerbread cookies.
## Grading Criteria.
- Any correct and justified solution - 7 points.
- Correct initial reasoning is provided, but incorrect conclusions are drawn or no conclusions are made - 2 points.
- The solution is complete, but one arithmetic error is made - 2 points.
- Only the correct answer - 1 point.
|
8
|
Number Theory
|
olympiads
| null | null |
\(\boxed{8}\)
|
Problem 9.7. The numbers $1, 2, 3, \ldots, 57$ are written on a board. What is the maximum number of these numbers that can be chosen so that no two chosen numbers differ exactly by a factor of 2.5?
|
Consider sequences of natural numbers that satisfy the following set of conditions: in each sequence
- each number does not exceed 57
- there are at least two numbers, and they all go in ascending order;
- each subsequent number is 2.5 times the previous one.
Let's list them all.
- 2,5
- $4,10,25$
- 6,15
- $8,20,50$
- 12,30
- 14,35
- 16,40
- 18,45
Notice that in each of these nine sequences, there should be at least one unselected number. Then the number of selected numbers is no more than $57-9=48$.
An example where the number of selected numbers is exactly 48 is not hard to construct: it is sufficient to select all numbers from 1 to 57, except for the second numbers from the nine sequences listed above.
|
48
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{48}\)
|
Problem 4.1. Along the road connecting Masha's and Sasha's houses, there are 17 apple trees and 18 poplars. When Masha was going to visit Sasha, she took photos of all the trees. Right after the tenth apple tree, Masha's phone memory ran out, and she couldn't photograph the remaining 13 trees. The next day, when Sasha was going to visit Masha, starting from the eighth apple tree, he picked one leaf from each tree. How many leaves did Sasha pick?
|
Note that the tenth apple tree, counting from Masha's house, is the eighth apple tree, counting from Sasha's house. Therefore, Sasha will not pick a leaf from exactly 13 trees. We get that he will pick a total of $17+18-13=22$ leaves.
|
22
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{22}\)
|
Problem 1. In the morning, 5 foreign cars were parked along the road. By noon, 2 domestic cars were parked between each pair of foreign cars. And by evening, a motorcycle was parked between each pair of adjacent cars. How many motorcycles were parked in total $?$
Answer: 12 .
|
Between 5 foreign cars there are 4 gaps, so there were $4 \cdot 2=8$ domestic cars parked there; that is, a total of $5+8=13$ cars were parked. Between them, 12 motorcycles were parked.
|
12
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{12}\)
|
Problem 2. At an open evening at the conservatory, four quartets, five duets, and six trios were supposed to perform (a quartet consists of four musicians, a trio of three, and a duet of two; each musician is a member of only one musical group). However, one quartet and two duets unexpectedly went on tour, and a soloist from one of the trios fell ill, so the members of this trio had to perform as a duo. How many musicians performed at the conservatory that evening?
|
If no one was absent, then at the evening there would have been
$4 \cdot 4(4$ quartets $)+5 \cdot 2(5$ duets $)+6 \cdot 3$ ( 6 trios $)=44$ people.
But $4(1$ quartet) $+2 \cdot 2$ (2 duets) +1 (a soloist from one of the trios) $=9$ people were absent. Thus, at the evening, $44-9=35$ people performed.
|
35
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{35}\)
|
Problem 4. Dima stood on one of the steps of the staircase and suddenly noticed that there were an equal number of steps above and below him. Then he climbed up 7 steps, and after that, he went down 15 steps. In the end, he found himself on the 8th step of the staircase (counting from the bottom). How many steps does the staircase consist of?
|
Since Dima ended up on the 8th step at the end, before that he was on the $8+15=23$ step. He got there by climbing up 7 steps, so he started from the $23-7=16$ step. Thus, we have that the 16th step is the middle of the ladder. Therefore, the ladder consists of 31 steps.
|
31
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{31}\)
|
Problem 6. Yulia thought of a number. Dasha added 1 to Yulia's number, and Anya added 13 to Yulia's number. It turned out that the number obtained by Anya is 4 times the number obtained by Dasha. What number did Yulia think of?
|
Note that since Anya's number is 4 times greater than Dasha's number, the difference between these numbers is 3 times greater than Dasha's number. Thus, Dasha's number is $(13-1): 3=4$. Therefore, Yulia's number is 3.
|
3
|
Algebra
|
olympiads
| null | null |
\(\boxed{3}\)
|
Problem 7. Aся, Borya, Vasilina, and Grisha bought tickets to the cinema for one row. It is known that:
- There are a total of 9 seats in the row, numbered from 1 to 9.
- Borya did not sit in seat 4 or 6.
- Aся sat next to Vasilina and Grisha, and no one sat next to Borya.
- There were no more than two seats between Aся and Borya.
In which seat, with what number, was someone definitely sitting?
Answer: 5.
|
Note that Asey, Vasilina, and Grisha occupy three seats in a row, and Borya sits one seat away from them. Let's seat another child, Dima, in the free seat. Then, 5 children sit in a row. Thus, someone is sitting in the central seat of the row (that is, seat number 5). For any other seat, we can come up with an arrangement such that it is not occupied.
What if Dima is sitting in the 5th seat? Then Borya (since they are sitting next to each other) must sit either in seat 4 or 6, but this contradicts the condition. Therefore, in seat 5, either Asey, Borya, Vasilina, or Grisha is sitting.
|
5
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{5}\)
|
Problem 8. Masha braided her dolls: half of the dolls got one braid each, a quarter of the dolls got two braids each, and the remaining quarter of the dolls got four braids each. She tied a ribbon in each braid. How many dolls does Masha have if she needed 24 ribbons in total?
|
Note that since a quarter of the dolls have four braids, the total number of ribbons used on them is the same as the total number of dolls. Half of the dolls have one braid, so the number of ribbons used on them is half the total number of dolls. And a quarter of the dolls have two braids, so the number of ribbons used on them is also half the total number of dolls.
This means that the number of ribbons is twice the number of dolls. Therefore, Masha has a total of 12 dolls.
|
12
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{12}\)
|
# 3. Option 1.
Vasya calculated two sums: the sum of consecutive odd numbers from 1 to 2021: $(1+3+5+\ldots+2021)$ and the sum of consecutive even numbers from 2 to 2020: $(2+4+6+\ldots+2020)$. After that, he subtracted the smaller sum from the larger one. What result did he get?
|
Let's find the difference between the sums of odd and even numbers: $(1+3+5+\ldots+2021)-(2+4+6+\ldots+2020)=(2021-2020)+(2019-2018)+\ldots+(3-2)+1=1011$.
|
1011
|
Algebra
|
olympiads
| null | null |
\(\boxed{1011}\)
|
# 8. Variant 1.
Each of the 10 students came up with 5 natural numbers. It turned out that each number was thought of by at least three students. What is the maximum number of different numbers that could have been thought of?
|
In total, the students came up with 50 numbers, with each number being counted at least 3 times. We will prove that there could not have been more than 16 different numbers. If at least 17 different numbers were thought of and each by at least three students, then a total of no less than $17 \cdot 3=51$ numbers were thought of. This is a contradiction. An example where 16 numbers were thought of: Suppose the numbers 1 and 2 were thought of by 4 students each, and numbers 3 to 16 were thought of by 3 students each. Then a total of $2 \cdot 4 + 14 \cdot 3 = 8 + 42 = 50$ numbers were thought of, and each by at least 3 students.
|
16
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{16}\)
|
4. Four friends came back from fishing. Every two of them counted the sum of their catches. Six numbers were obtained: $7,9,14,14,19,21$. How many fish were caught in total?
|
fish.
Note that the catch of each person is counted in exactly three sums. Therefore, if we add up all six numbers, we get the tripled total catch. Thus, the total number of fish caught is $(7+9+14+14+19+21): 3=28$ fish.
|
28
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{28}\)
|
6.1. Find the largest six-digit number, all digits of which are different, and each of the digits, except for the extreme ones, is either the sum or the difference of the adjacent digits.
|
Let $A$ be the desired number. Let's try to find the number $A$ with the first digit being 9. We will try different options for the second digit. If the second digit is 8, then we get: $A=98176-$ it does not form a six-digit number. If the second digit is 7, then we get: $A=972538-$ a six-digit number.
Comment. Just the correct answer, but attempts to find the maximum number are missing - 4 points.
Any incorrect answer - 0 points.
|
972538
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{972538}\)
|
11.1 A quirky person didn't mind the effort and recorded 2023 numbers in a circle such that each number is equal to the product of its two neighbors. What is the maximum number of different numbers that could have been used?
|
If there is a zero among the numbers, then its neighbors are also zeros, so all the recorded numbers will be equal to zero. We will assume that there are no zeros among the numbers. Let $a$ and $b$ be two adjacent numbers. Then on the other side of $a$ stands $a / b$, and on the other side of $b$ stands $b / a$. In other words, two numbers at a distance of 3 are reciprocals of each other, and then numbers at a distance of 6 are equal. Since 2023 is coprime with 6, it follows that all numbers are equal in any case.
## Criteria:
- Only the answer with an example - 0 points.
- Points are not deducted for the absence of an example where all numbers are equal.
|
1
|
Algebra
|
olympiads
| null | null |
\(\boxed{1}\)
|
4. Dwarves Glóin, Óin, and Thráin found 70 identical precious stones and want to divide them among themselves so that each of them gets no less than 10 stones. In how many ways can the dwarves do this?
|
Give each dwarf 9 stones, and lay out the remaining 43 stones in a row. To distribute the remaining stones among the dwarves, it is sufficient to place two dividers in the 42 spaces between the stones. Gloin will receive the stones to the left of the first divider, Oin will receive the stones between the two dividers, and Thrain will receive the stones to the right of the second divider. The number of ways to place these two dividers is $\frac{42 \cdot 41}{2}=861$.
Comment: Deduct 1 point for a computational error with correct reasoning. Deduct 1-2 points for potentially useful but unimplemented ideas.
|
861
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{861}\)
|
1. (7 points) Replace each letter with a digit so that the operations performed horizontally and vertically are valid.
| $a b$ | + | $c d$ | $=$ | $e f$ |
| :---: | :---: | :---: | :---: | :---: |
| $\times$ | | $:$ | | + |
| $k$ | $:$ | $m$ | $=$ | $m$ |
| $m n d$ | $:$ | $e$ | $=$ | $e m$ |
Identical letters correspond to identical digits.
|
# Solution.
| 42 | + | 18 | $=$ | 60 |
| :---: | :---: | :---: | :---: | :---: |
| $\times$ | | $:$ | | + |
| 9 | $:$ | 3 | $=$ | 3 |
| 378 | $:$ | 6 | $=$ | 63 |
|
63
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{63}\)
|
2. A three-digit number, all digits of which are different, will be called balanced if it is equal to the sum of all possible two-digit numbers formed from the different digits of this number. Provide an example of any balanced number. Justify your answer.
|
For example, the number $132=13+12+32+21+31+23$ is balanced (there are other options).
Grading criteria: Any suitable number with verification - 7 points, incorrect solution or only answer - 0 points.
|
132
|
Number Theory
|
olympiads
| null | null |
\(\boxed{132}\)
|
Problem 8.1. Gleb placed the numbers $1,2,7,8,9,13,14$ at the vertices and the center of a regular hexagon such that in any of the 6 equilateral triangles, the sum of the numbers at the vertices is divisible by 3. What number could Gleb have written in the center? It is sufficient to provide one suitable example.
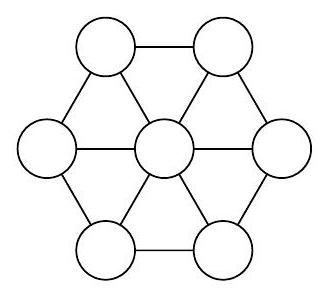
|
Let's add the sums of the numbers in all six triangles; denote this value by $X$. On the one hand, $X$ is divisible by 3, since each term was divisible by 3 according to the condition. On the other hand, each number at the vertex of the hexagon entered $X$ twice (from two triangles), and the central number entered it 6 times. Subtracting from $X$ twice the sum of all numbers, which is $2 \cdot 54$, we get the quadrupled central number.
Divisibility by 3 is preserved in this process. This means that the number in the center is a multiple of 3. We have only one such number, which is 9.
The other numbers can be arranged around the perimeter of the hexagon so that their remainders when divided by 3 alternate; for example, in the order $1,2,7,8,13,14$.
|
9
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{9}\)
|
Problem 8.2. Misha suggested that Yulia move a chip from cell $A$ to cell $B$. In one step, you can move the chip to an adjacent cell by side or by corner. To make it more interesting, Misha put 30 candies in the prize fund, but said that he would take 2 candies for each horizontal or vertical move and 3 candies for each diagonal move. The remaining candies Yulia gets as a reward. What is the maximum number of candies Yulia can win?
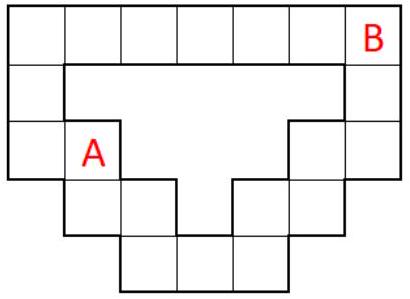
|
From $A$ to $B$, one can get through the top or the bottom. If going through the top, the first 2 moves are diagonal (a diagonal move is more advantageous than 2 horizontal moves), and the next 5 moves are horizontal. Misha will take $2 \cdot 3 + 5 \cdot 2 = 16$ candies, and Yulia will win 14. If going through the bottom, the first 5 moves are diagonal, and the last move is vertical. In this case, Misha will take $5 \cdot 3 + 1 \cdot 2 = 17$ candies, and Yulia will win 13 candies. We get that the first option is more advantageous, and the win will be 14 candies.
|
14
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{14}\)
|
Problem 8.5. A field was partially planted with corn, oats, and millet. If the remaining part is completely planted with millet, then millet will occupy half of the entire field. If the remaining part is equally divided between oats and corn, then oats will occupy half of the entire field. By what factor will the amount of corn increase if the remaining part is completely planted with corn?
|
Let the area of the entire field be 1, and the empty part be $x$. Then, from the first condition, millet occupies $\frac{1}{2}-x$, and from the second condition, oats occupy $\frac{1}{2}-\frac{1}{2} x$.
Corn is left with $1-x-\left(\frac{1}{2}-x\right)-\left(\frac{1}{2}-\frac{1}{2} x\right)=\frac{1}{2} x$. If we add $x$ to this, we get $\frac{3}{2} x$, which means the area planted with corn will triple.
|
3
|
Algebra
|
olympiads
| null | null |
\(\boxed{3}\)
|
Problem 8.6. Six princesses have a magic chest. Every minute, a dress of one of 10 colors and one of 9 styles can be taken out of it. However, within one hour, it is impossible to take out two dresses from the chest that match both in color and style. What is the minimum number of dresses the princesses will have to take out of the chest to guarantee getting 6 dresses of different colors in one style?
|
Note that 45 dresses would not be enough, as the chest can issue exactly 5 dresses of each of the 9 styles.
We will prove that if the princesses take out 46 dresses, there will definitely be 6 dresses of the same style, and thus of different colors (identical dresses could not have occurred over the 46 minutes). Indeed, if this were not the case, then there would be no more than 5 dresses of each style, meaning there would be no more than 45 dresses in total; a contradiction.
|
46
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{46}\)
|
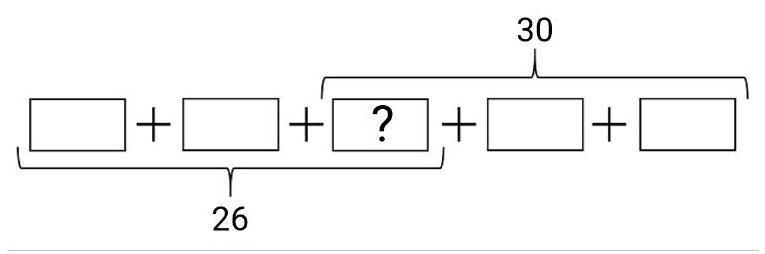
Problem 6.1. The set includes 8 weights: 5 identical round, 2 identical triangular, and one rectangular weight weighing 90 grams.
It is known that 1 round and 1 triangular weight balance 3 round weights. Additionally, 4 round weights and 1 triangular weight balance 1 triangular, 1 round, and 1 rectangular weight.
How much does the triangular weight weigh?
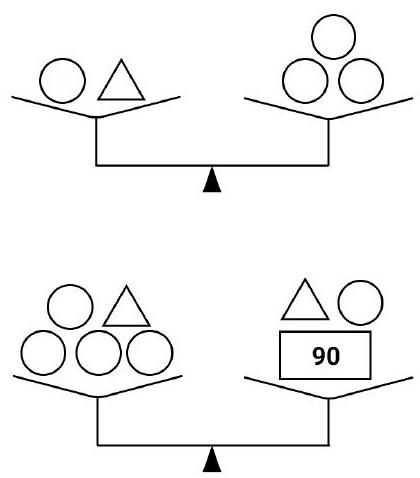
|
From the first weighing, it follows that 1 triangular weight balances 2 round weights.
From the second weighing, it follows that 3 round weights balance 1 rectangular weight, which weighs 90 grams. Therefore, a round weight weighs $90: 3=30$ grams, and a triangular weight weighs $30 \cdot 2=60$ grams.
|
60
|
Algebra
|
olympiads
| null | null |
\(\boxed{60}\)
|
2.1. The numbers 7, 8, 9, 10, 11 are arranged in a row in some order. It turned out that the sum of the first three of them is 26, and the sum of the last three is 30. Determine the number standing in the middle.
|
If we add the sum of the first three and the sum of the last three, we get the sum of all four numbers once and the middle number twice. Since the sum of all five numbers is $7+8+9+10+11=45$, and the sum of 26 and 30 is 56, then the number counted twice is 11.
|
11
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{11}\)
|
3.1. Every day, a sweet tooth buys one more candy than the previous day. In one week, on Monday, Tuesday, and Wednesday, he bought a total of 504 candies. How many candies did he buy on Thursday, Friday, and Saturday in total for the same week?
|
On Thursday, 3 more candies were bought than on Monday, on Friday - 3 more than on Tuesday, and on Saturday - 3 more than on Wednesday. In total, 9 more candies were bought on Thursday, Friday, and Saturday compared to Monday, Tuesday, and Wednesday, i.e., $504+9=513$ candies.
|
513
|
Algebra
|
olympiads
| null | null |
\(\boxed{513}\)
|
5.1. Alina travels to school by bus. The bus runs on a schedule every 15 minutes. It always takes the girl the same number of minutes to get to the bus stop. If she leaves home at 8:20, she will be at school at 8:57, but if she leaves home at 8:21, she will be late for school. Classes start at 9:00. How many minutes will Alina be late for school if she leaves home at 8:23?
|
Since Alina is late for school if she leaves home one minute after 8:20, leaving 1, 2, ... 15 minutes after 8:20, she will catch the next bus, which means she will arrive at school 15 minutes later than 8:57, i.e., she will arrive at school at 9:12.
|
12
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{12}\)
|
7.5. A hundred people are standing in a circle, each of whom is either a knight or a liar (liars always lie, and knights always tell the truth). Each of those standing said: “I have a liar as a neighbor.” Find the minimum possible number of liars among these 100 people.
|
Note that 3 knights cannot stand next to each other, as in this case, the middle knight would be lying. Therefore, among any 3 standing next to each other, there is a liar. Take any liar, and divide the remaining 99 people into 33 groups of three standing next to each other. Since there is at least one liar in each group of three, the total number of liars in the circle is no less than $1+33=34$.
Exactly 34 liars can stand, for example, as follows: -L(KLK)(KLK)... (KLK)-.
Comment: It is only proven that the number of liars is no less than $34-4$ points.
Only an example of an arrangement with 34 liars is given -2 points.
|
34
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{34}\)
|
3. Sasha invited Dima to visit, saying that he lives in entrance 10, apartment No. 333, but forgot to mention the floor. Approaching the building, Dima noticed that the building is nine-story. Which floor should he go to?
|
$333=9 \cdot 37=10 \cdot 33+3$. Therefore, the number of apartments in the entrance is less than 37 but more than 33. In this range, only 36 is divisible by 9. So, there are 36 apartments in the entrance, and 4 on each floor. Since $333=9 \cdot 36+2 \cdot 4+1$, apartment 333 is on the third floor.
|
3
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{3}\)
|
9.2. The graphs of the functions $y=a x^{2}+b x+1$ and $y=x^{2}+c x+d$ intersect at the point with coordinates ( $2 ; 4$ ). What is the value of the expression $4 a+d$, if $b+c=1$ ?
|
Since the graphs pass through the point with coordinates (2; 4), then $4=4a+2b+1$ and $4=4+2c+d$. Therefore, $4a+2b=3$, and $2c+d=0$, or $4a=3-2b, d=-2c$. Summing up the obtained expressions: $4a+d=3-2b-2c=3-2(b+c)=3-2=1$. Note: The condition is satisfied by the functions $y=ax^2+bx+1$ and $y=x^2+cx+d$ when $a=1, b=-1/2, c=3/2, d=-3$.
Criteria: Only the answer - 0 points. If the solution is found by selecting suitable values of $a, b, c$ and $d-3$ points. Correctly found values of the expressions $4a+2b=3$ and $2c+d=0$, but no further progress in the solution (or incorrect further solution) - 4 points. 7 points for a complete and correct solution.
|
1
|
Algebra
|
olympiads
| null | null |
\(\boxed{1}\)
|
11.1. In a six-digit number, the first digit, which is 2, was moved to the last place, leaving the other digits in the same order. The resulting number turned out to be three times larger than the original. Find the original number.
|
According to the condition, the desired number has the form $\overline{2 a b c d e}$, then we have: $\overline{a b c d e 2}=$ $3 \cdot \overline{2 a b c d e}$, or $\overline{a b c d e} \cdot 10+2=3 \cdot(200000+\overline{a b c d e})$. Let $\overline{a b c d e}=X$ - a five-digit number, then $10 X+2=3 \cdot(200000+X)$, or $7 X=600000-2, X=85714$, then the original number will be $\overline{2 a b c d e}=\overline{2 X}=285714$.
|
285714
|
Number Theory
|
olympiads
| null | null |
\(\boxed{285714}\)
|
Problem 7.2. Each of the natural numbers $1,2,3, \ldots, 377$ is painted either red or blue (both colors are present). It is known that the number of red numbers is equal to the smallest red number, and the number of blue numbers is equal to the largest blue number. What is the smallest red number?
|
Let $N$ be the largest blue number. Then only numbers from 1 to $N$ can be painted blue. Since there are a total of $N$ blue numbers, we get that all numbers from 1 to $N$ are blue. Accordingly, all numbers from $N+1$ to 377 are red. Since the number of red numbers equals the smallest red number, we get the equation $N+1=377-N$, from which we find $N=188$. Therefore, the smallest red number is 189.
|
189
|
Number Theory
|
olympiads
| null | null |
\(\boxed{189}\)
|
Problem 7.3. Krosh and Yozhik decided to check who would run faster along a straight road from Kopyatych's house to Losyash's house. When Krosh had run 20 meters, Yozhik had run only 16 meters. And when Krosh had 30 meters left, Yozhik had 60 meters left. How many meters is the length of the road from Kopyatych's house to Losyash's house? (Krosh and Yozhik started running at the same time, each running at their own constant speed.)
|
When Krosh ran 20 meters, Yozhik ran only 16 meters, so their speeds are in the ratio of $5: 4$.
When Krosh had 30 meters left to run, let him have already run $5 x$ meters (where $x$ is not necessarily an integer). Then by this point, Yozhik had run $4 x$ meters. Therefore, the total length of the entire path in meters is on one side $5 x+30$, and on the other side $4 x+60$. We get the equation $5 x+30=4 x+60$, from which we find $x=30$.
Therefore, the desired length is $5 \cdot 30+30=180$ meters.
|
180
|
Algebra
|
olympiads
| null | null |
\(\boxed{180}\)
|
Problem 5.2. During a physical education class, 25 students from 5B class lined up. Each of the students is either an excellent student who always tells the truth, or a troublemaker who always lies.
Excellent student Vlad stood in the 13th place. Everyone except Vlad stated: "There are exactly 6 troublemakers between me and Vlad." How many troublemakers are there in the line?
|
Note that students in places $7-12$ are troublemakers, since there are fewer than 6 people between each of them and Vlad. Therefore, the student with number 6 is an excellent student. The same can be said about the student in the 5th place, then about the 4th, the 3rd, the 2nd, and the 1st.
Thus, the first six places are occupied by excellent students, the next six places are occupied by troublemakers, and Vlad is already at place 13. Similar reasoning can be applied to students in places $14-25$. Therefore, there are exactly $6+6=12$ troublemakers in the line.
|
12
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{12}\)
|
Problem 5.5. Denis has identical ten-ruble coins, identical two-ruble coins, and identical one-ruble coins (more than 20 coins of each type). In how many ways can Denis pay exactly 16 rubles for a pie without receiving change? It is not necessary to use coins of each type.
|
If Denis uses a ten-ruble coin, he will need to collect 6 rubles using two-ruble and one-ruble coins. There are 4 ways to do this: using from 0 to 3 two-ruble coins.
If Denis does not use the ten-ruble coin, he will need to collect 16 rubles using two-ruble and one-ruble coins. There are 9 ways to do this, using from 0 to 8 two-ruble coins.
In total, there are $4+9=13$ ways.
|
13
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{13}\)
|
5.1. 20 schoolchildren came to the mathematics Olympiad. Everyone who brought a pencil also brought a pen. 12 people forgot their pencils at home, and 2 schoolchildren forgot their pen. By how many fewer schoolchildren brought a pencil than those who brought a pen but forgot a pencil?
|
students brought a pencil, which means they also brought a pen. 18 students brought a pen. Therefore, 10 students brought a pen without a pencil. Then 10-8=2.
|
2
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{2}\)
|
1. 1.1. An online electric scooter rental service charges a fixed amount for a ride and a certain amount for each minute of rental. Katya paid 78 rubles for a ride lasting 3 minutes. Lena paid 108 rubles for a ride lasting 8 minutes. It takes Kolya 5 minutes to get from home to work. How much will he pay for this ride?
|
## Solution.
1st method. If the rental of a scooter costs $x$ rubles, and a minute of use costs $y$ rubles, then $x+3y=78$, and $x+8y=108$. Solving this system, we get that $y=6, x=60$. Then Kolya will pay $60+30=90$ rubles.
2nd method. Notice that Lena's trip is 30 rubles more expensive than Katya's trip and lasts 5 minutes longer. It turns out that 1 minute, not counting the rental cost, is $30:5=6$ rubles. Then, since Katya paid 78 rubles for 3 minutes, $78-3 \times 6=60$ rubles. Therefore, Kolya paid $60+30=90$ rubles.
|
90
|
Algebra
|
olympiads
| null | null |
\(\boxed{90}\)
|
2. 2.1. Dealer Dima bought a "LADA Kalina" car from the manufacturer and increased its price by $A \%$. There was no demand, and Dima had to sell the car at a sale with a $20 \%$ discount. As a result, his profit was $20 \%$. Find $A$.
|
## Solution.
1st method. Let's assume Dima bought a car from the manufacturer for $X$ rubles. After raising the price, the car cost $X(1+A / 100)$ rubles. After reducing the price by $20 \%$, the car cost $0.8 X(1+A / 100)$. According to the condition, this is the same as $1.2 X$. Therefore, $1+A / 100=1.2 / 0.8$, which means $A=50$.
2nd method. After increasing by A\%, the price increased by ( $1+A / 100$ ) times. After reducing the price by $20 \%$, the price is multiplied by 0.8 and becomes 1.2 times the purchase price. Then, $(1+A / 100) \cdot 0.8=1.2$. Therefore, $1+A / 100=1.2: 0.8=1.5$, from which $=50$.
|
50
|
Algebra
|
olympiads
| null | null |
\(\boxed{50}\)
|
2.1. Petya writes on the board such different three-digit natural numbers that each of them is divisible by 3, and the first two digits differ by 2. What is the maximum number of such numbers he can write if they end in 6 or 7?
|
A number is divisible by 3 if the sum of its digits is a multiple of 3. If the number ends in 6, then the sum of the other two digits leaves a remainder of 0 when divided by 3. Such numbers are: 2,4 and 4,2; 5,7 and 7,5. If the number ends in 7, then the sum of the other two digits leaves a remainder of 2 when divided by 3. Such numbers are: 2,0; 3,5 and 5,3; 6,8 and 8,6. In total, there are 9 numbers: 246, 426, 576, 756, 207, 357, 537, 687, 867.
|
9
|
Number Theory
|
olympiads
| null | null |
\(\boxed{9}\)
|
3.1. Every hour, between two adjacent nettle bushes in a row, two more of the same grow. How many bushes do you need to plant initially so that after three hours, the total number of bushes together is 190?
|
If at the moment there are $\mathrm{n}$ bushes, then on the next move their number increases by $2(n-1)$. Thus, if after 3 hours the total number of bushes should be 190, then one hour before that, there should be $\frac{190-1}{3}+1=64$. One more hour back, $\frac{64-1}{3}+1=22$. And on the next move $\frac{22-1}{3}+1=8$.
|
8
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{8}\)
|
5.1. 40 people came into a room where there were 40 chairs, black and white, and sat on them. All of them said they were sitting on black chairs. Then they somehow resat, and exactly 16 claimed they were sitting on white chairs. Each of those sitting either lied both times or told the truth both times. How many of them lied the second time and were sitting on black chairs?
|
Initially, everyone who told the truth sat on black chairs, and everyone who lied sat on white ones. After some of them switched chairs, 16 claimed they were sitting on white chairs. Obviously, this group includes those who told the truth and were sitting on white chairs, and those who switched with them - they lied and were sitting on black chairs. Since their numbers are equal, exactly half of them - 8 - lied and were sitting on black chairs.
|
8
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{8}\)
|
2. When adding two integers, a student mistakenly added an extra zero at the end of the second addend and got a sum of 7182 instead of 3132. Determine the addends.
#
|
# Solution
By subtracting the second sum from the first, we find the second addend multiplied by 9. Thus, the required numbers are 2682 and 450.
## Grading Criteria
The numbers are correct, but the method of obtaining them is not specified - 1 point.
The correct answer is obtained with a valid explanation - 7 points.
|
2682450
|
Algebra
|
olympiads
| null | null |
\(\boxed{2682450}\)
|
10.4. Find $f(2021)$ if for any real $x$ and $y$ the equality $f(x+f(y))=x+y$ holds.
|
Let $f(0)=b$, then for $y=0$ we get $f(x+b)=x$, from which $f(x)=x-b$. Thus, $f(x+f(y))=f(x+(y-b))=f(x+y-b)=x+y-b-b=x+y-2b$.
Since $f(x+f(y))=x+y$ for any real $x$ and $y$, then $b=0$, so $f(x)=x$, and $f(2021)=2021$.
Comment. Only the example of the function $f(x)=x-1$ gets a point.
|
2021
|
Algebra
|
olympiads
| null | null |
\(\boxed{2021}\)
|
1. Find the smallest 10-digit number, the sum of whose digits is not less than that of any smaller number.
|
Among 9-digit numbers, the largest sum of digits is for the number 999999999, which is 81. Since the desired 10-digit number is greater than 999999999, we need to find the smallest number with a sum of digits no less than 81. The sum of the last eight digits of the desired number is no more than $9 \cdot 8=72$, so the sum of the first two digits is no less than $81-72=9$. Since the desired number is the smallest, its first digit is 1, and the second digit is 8. Then the sum of the remaining eight digits is no less than 72, which means the remaining digits are nines.
Criteria. Correct answer without explanation - 1 point. Proven that the sum of the digits of the desired number is no less than $81-3$ points. Complete solution - 7 points.
|
1899999999
|
Number Theory
|
olympiads
| null | null |
\(\boxed{1899999999}\)
|
.2. On the table, there are 30 coins: 23 ten-ruble coins and 7 five-ruble coins, with 20 of these coins lying heads up and the remaining 10 tails up. What is the smallest $k$ such that among any $k$ randomly selected coins, there will definitely be a ten-ruble coin lying heads up?
|
If you choose 18 coins, then among them there will be no more than 10 lying heads down, so at least 8 coins will be lying heads up. Among these coins, no more than 7 will be five-ruble coins, so at least one will be a ten-ruble coin, which is what we need.
On the other hand, if initially on the table there are 7 five-ruble coins heads up, 10 ten-ruble coins heads down, and 13 ten-ruble coins heads up, then among 17 coins there might be only coins of the first two types, so 17 coins (or fewer) might not be enough.
|
18
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{18}\)
|
Problem 11.3. The product of positive numbers $a$ and $b$ is 1. It is known that
$$
(3 a+2 b)(3 b+2 a)=295
$$
Find $a+b$.
|
Expanding the brackets, we get
$$
295=6 a^{2}+6 b^{2}+13 a b=6\left(a^{2}+b^{2}\right)+13
$$
from which $a^{2}+b^{2}=47$. Then
$$
(a+b)^{2}=a^{2}+b^{2}+2 a b=47+2=49=7^{2}
$$
which gives $a+b=7$ (note that $a+b>0$, since $a>0$ and $b>0$).
|
7
|
Algebra
|
olympiads
| null | null |
\(\boxed{7}\)
|
4. In a company of 8 people, each person is acquainted with exactly 6 others. In how many ways can four people be chosen such that any two of them are acquainted? (We assume that if A is acquainted with B, then B is also acquainted with A, and that a person is not acquainted with themselves, as the concept of acquaintance applies to two different people.)
|
Each person in the company does not know $8-1-6=1$ person in this company. This means the company can be divided into four pairs of strangers. From each pair, we can only take one person to form a company of four people who are all acquainted with each other. The selection of such a company consists of four steps, each with two choices (from each pair), and by the multiplication rule, the company can be chosen in $2^{4}=16$ ways.
Criteria. It is shown that each person is not acquainted with exactly one of the others and only: 1 point.
It is indicated that exactly one person must be chosen from each pair of strangers, but the calculations are incorrect: 3 points.
|
16
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{16}\)
|
3. For what value of the parameter m is the sum of the squares of the roots of the equation
$$
x^{2}-(m+1) x+m-1=0
$$
the smallest?
|
$\mathrm{m}=3$.
Note that the discriminant $\mathrm{D}$ of the equation is equal to
$$
\mathrm{D}=(\mathrm{m}+1)^{2}-4(\mathrm{~m}-1)=(\mathrm{m}-1)^{2}+4>0
$$
therefore, the equation has two roots for any $\mathrm{m}$. Let's represent the sum of the squares of the roots $\mathrm{x}_{1}$ and $\mathrm{x}_{2}$ as
$$
x_{1}^{2}+x_{2}^{2}=\left(x_{1}+x_{2}\right)^{2}-2 x_{1} x_{2}
$$
From Vieta's theorem, we get
$$
x_{1}^{2}+x_{2}^{2}=\frac{(m+1)^{2}}{4}-2(m-1)
$$
The minimum value of $x_{1}^{2}+x_{2}^{2}$ is achieved at the minimum point of the function $\mathrm{f}(\mathrm{m})=(\mathrm{m}+1)^{2}-8(\mathrm{~m}-1)$, which is $\mathrm{m}_{\min }=3$.
|
3
|
Algebra
|
olympiads
| null | null |
\(\boxed{3}\)
|
5.1. It is known that in the past chess tournament, in each round all players were paired, the loser was eliminated (there were no draws). It is known that the winner played 6 games. How many participants in the tournament won at least 2 games more than they lost?
|
Since the winner played 6 games, there were a total of $2^{6}=64$ players. The win-loss ratio for those eliminated in the 1st round is -1; for those who lost in the 2nd round, it is 0; for those who lost in the 3rd round, it is +1; for those who lost in the 4th round and beyond, it is at least +2. 8 participants reached the $4th$ round.
|
8
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{8}\)
|
6.1. In a basketball team, there is a certain number of players. The coach added up all their heights and divided by the number of players (let's call this the average height), getting 190 cm. After the first game, the coach removed Nikolai, who is 197 cm tall, and replaced him with Petr, who is 181 cm tall, after which the average height of the players in the team was 188 cm. How many people are in the team?
|
The change in the total height of the players by $197-181=16$ cm leads to a change in the average height of the team by $190-188=2$ cm, so the team has $\frac{16}{2}=8$ people.
|
8
|
Algebra
|
olympiads
| null | null |
\(\boxed{8}\)
|
1. A flask contains 40 liters of milk. How can you transfer 6 liters of milk from it into a 10-liter bucket using a 9-liter and a 5-liter bucket?
|
We fill the 5-liter bucket with milk and pour it into the bucket. Then we fill the 5-liter bucket again, pour it into the 9-liter bucket, fill the 5-liter bucket once more, and pour the missing 4 liters into the 9-liter bucket. Then, exactly 1 liter remains in the 5-liter bucket, which we pour into the bucket.
|
6
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{6}\)
|
Problem 6.1. The set includes 8 weights: 5 identical round, 2 identical triangular, and one rectangular weight weighing 90 grams.
It is known that 1 round and 1 triangular weight balance 3 round weights. Additionally, 4 round weights and 1 triangular weight balance 1 triangular, 1 round, and 1 rectangular weight.
How much does the triangular weight weigh?
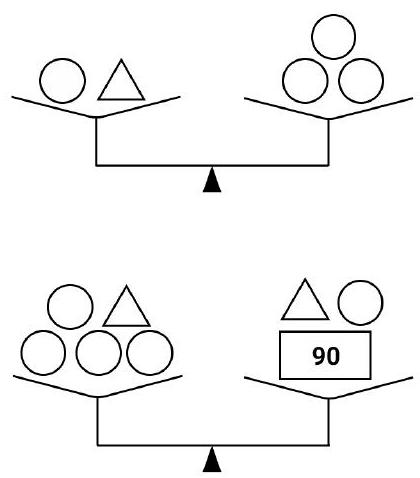
|
From the first weighing, it follows that 1 triangular weight balances 2 round weights.
From the second weighing, it follows that 3 round weights balance 1 rectangular weight, which weighs 90 grams. Therefore, a round weight weighs $90: 3=30$ grams, and a triangular weight weighs $30 \cdot 2=60$ grams.
|
60
|
Algebra
|
olympiads
| null | null |
\(\boxed{60}\)
|
1. The number 1232 is divisible by the sum of its digits $1+2+3+2=8$. What is the next number that is divisible by the sum of its digits?
|
One can notice that the next number fits, as 1233 is divisible by the sum of its digits $1+2+3+3=9$. Indeed, $1233: 9=137$.
Comment: One could have avoided performing the division and instead used the divisibility rule for 9.
|
1233
|
Number Theory
|
olympiads
| null | null |
\(\boxed{1233}\)
|
2. Vasya constructed a robot, but he messed up the program, so the robot makes random moves that somehow always lead it to the right point.
A move is a one-kilometer displacement either north (N), east (E), south (S), or west (W).
The robot reached its goal in 22 moves:
# EENENNWNENESEEEEESSSWN.
How many moves would the robot need if it did not make any extra moves?
|
Let's count the number of each type of letter. $E$ appears 10 times, $W-2$ times, $N-6$ times, $S-$ 4 times. In total, the robot's goal is to move 8 km east and 2 km north. Therefore, without extra moves, the route would consist of $8+2=10$ moves.
|
10
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{10}\)
|
3. A farmer wants to start growing watermelons. He wants to sell at least 10,000 watermelons every year. Watermelons are grown from seeds (one seed grows into one watermelon). Each watermelon can produce 250 good seeds that can be planted the following year, but then this watermelon cannot be sold. What is the minimum number of watermelon seeds the farmer should buy to start growing watermelons, and never have to buy seeds again?
|
Let the smallest number of seeds the farmer needs to buy be $10000+x$. Then he will be able to sell 10000 watermelons, and the remaining $x$ watermelons can be used for seeds. For the seeds to be sufficient for the next season, the inequality $250 x \geqslant 10000+x$ must hold. From this, $x \geqslant \frac{10000}{249}=40 \frac{40}{249}$. Therefore, $x=41$.
|
10041
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{10041}\)
|
4. For the function $f(x)$, it is known that it is odd, i.e., $f(-x) = -f(x)$ for every real $x$. Additionally, it is known that for every $x$, $f(x+5) = f(x)$, and also $f(1 / 3) = 2022$, and $f(1 / 2) = 17$. What is the value of
$$
f(-7) + f(12) + f\left(\frac{16}{3}\right) + f\left(\frac{9}{2}\right) ?
$$
|
Let's find the values of $f(-7)+f(12)$, $f\left(\frac{16}{3}\right)$, and $f\left(\frac{9}{2}\right)$ separately.
- $f(-7)+f(12)=f(-7+5)+f(12-2 \cdot 5)=f(-2)+f(2)=0$;
- $f\left(\frac{16}{3}\right)=f\left(5+\frac{1}{3}\right)=f\left(\frac{1}{3}\right)=2022$.
- $f\left(\frac{9}{2}\right)=f\left(5-\frac{1}{2}\right)=f\left(-\frac{1}{2}\right)=-f\left(\frac{1}{2}\right)=-17$
The answer is $0+2022-17=2005$.
|
2005
|
Algebra
|
olympiads
| null | null |
\(\boxed{2005}\)
|
6. For the numbers $1000^{2}, 1001^{2}, 1002^{2}, \ldots$, the last three digits are discarded. How many of the first terms of the resulting sequence form an arithmetic progression?
|
$(1000+k)^{2}=1000000+2000 k+k^{2}$. As long as $k^{2}<1000$, after discarding the last three digits, the number $1000+2 k$ will remain, i.e., each term of the sequence will be 2 more than the previous one. When $k=31: k^{2}=961<1000$, and when $k=32: k^{2}=1024$. Therefore, the element obtained from $1032^{2}$ will differ from the previous one by 3. Thus, the length of the progression is the number of numbers from 1000 to 1031, i.e., 32.
|
32
|
Number Theory
|
olympiads
| null | null |
\(\boxed{32}\)
|
2. The numbers from 1 to 8 are arranged in a circle. A number is called large if it is greater than its neighbors, and small if it is less than its neighbors. Each number in the arrangement is either large or small. What is the greatest possible sum of the small numbers?
|
Instructions. Adjacent numbers cannot be of the same type, so large and small numbers alternate, and there are four of each. 8 is large. 7 is also large, since a small number must be less than two numbers, and seven is less than only one. 1 and 2 are small. 6 and 5 cannot both be small, as they are less than only two numbers, and they cannot be adjacent in this case. Therefore, the sum of the two other small numbers (besides 1 and 2) is no more than 10. And the sum of the small numbers is no more than 13. Example: $8,6,7,1,3$, $2,5,4$.
Criteria. Only the correct answer and example: 2 points.
|
13
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{13}\)
|
9.2 In Pokémon hunting, 11 adults and $n$ children participated. Together, they caught $n^{2}+3 n-2$ Pokémon, with all adults catching the same number, and all children catching the same number, but each child catching 6 fewer than an adult. How many children participated in the game?
|
Let each child catch $m$ pokemons. Then $n m+11(m+6)=n^{2}+3 n-2$. From this, $(n+11) m=n^{2}+3 n-68$. Therefore, the right side is divisible by $n+11$. We have $n^{2}+3 n-68=$ $n(n+11)-8(n+11)+20$, so 20 is divisible by $n+11$. The only divisor of 20 greater than 10 is 20 itself, so $n+11=20, n=9$.
## Criteria:
- No points are deducted for the lack of an example for $n=9$.
- It is shown that $n=9$ works, but it is not proven that there are no other options -1 point.
|
9
|
Algebra
|
olympiads
| null | null |
\(\boxed{9}\)
|
2. Masha drew a rhombus in her notebook and wrote four numbers at the vertices, the sum of which is 2021. Then she wrote the product of the numbers at the ends of each side of the rhombus and calculated the sum of the numbers written on the sides. Katya increased all the numbers written by Masha at the vertices by 1, and then repeated what Masha did and calculated the new sum of the numbers on the sides. By how much is Katya's sum greater than Masha's?
|
Let Masha write the numbers $a, b, c, d$ at the vertices of the rhombus, then $a+b+c+d=2021$, and she obtained the sum of the products
$$
a b+b c+c d+d a=(a+c)(b+d)
$$
Since Katya increased each number by 1, her sum is
$$
(a+c+2)(b+d+2)=(a+c)(b+d)+2(a+b+c+d)+4
$$
greater than Masha's by $2(a+b+c+d)+4=2 \cdot 2021+4=4046$.
Criteria. Full solution - 7 points. Considered a particular case with the correct answer - 1 point. Only answer - 0 points.
|
4046
|
Algebra
|
olympiads
| null | null |
\(\boxed{4046}\)
|
8.2. Biathletes Arina and Lisa start on the same distance. Their starting numbers are two-digit numbers with the following peculiarity: if the sum of the digits of the starting number is added to the square of the difference of the digits of the number, the result is this number. Find the starting numbers of Arina and Lisa. (7 points)
#
|
# Solution.
Let 10a+b be the desired number. According to the condition $\mathrm{a}+\mathrm{b}+(\mathrm{a}-\mathrm{z})^{2}=10 \mathrm{a}+\mathrm{b}$ or $(a-в)^{2}=9 a$, from which it follows that $a-$ is a perfect square.
By checking the three cases ( $a=1, \mathrm{a}=4$ and $\mathrm{a}=9$ ), we get two solutions: 14 and 90.
Comment
|
1490
|
Number Theory
|
olympiads
| null | null |
\(\boxed{1490}\)
|
3. Find the largest natural number $\mathrm{n}$, for which the system of inequalities
$1<x<2, 2<x^{2}<3, \ldots, n<x^{n}<n+1$
has a solution. (6 points)
|
From the condition $: n=4$.
Rewrite the inequalities as:
$\left\{\begin{aligned} & 16^{3} \text{, then for } n=5 \text{ the given system is already inconsistent: the intervals } [\sqrt[3]{3}, \sqrt[4]{4}] \text{ and } [\sqrt[5]{2}, \sqrt[5]{6}] \text{ do not intersect.} \\ & \text{For } n=4 \text{, it is not difficult to find a value of } x \text{ that satisfies all four inequalities (for example, } x=1.45 \text{).} \end{aligned}\right.$
|
4
|
Inequalities
|
olympiads
| null | null |
\(\boxed{4}\)
|
11.3. The numbers $a_{1}, a_{2}, a_{3}, a_{4}$ and $a_{5}$ form a geometric progression. Among them, there are both rational and irrational numbers. What is the maximum number of terms in this progression that can be rational numbers?
|
Example: let $a_{1}=1, q=\sqrt{2}$, we get the geometric progression $1, \sqrt{2}, 2, 2\sqrt{2}, 4$. Evaluation. If there are 4 rational numbers among them, then there will be two consecutive rational members of the geometric progression. This means that the common ratio of the progression (the ratio of the subsequent term to the previous one) is a rational number. But then, with a rational $a_{1}$, all terms of the progression are rational numbers, and with an irrational $a_{1}$, all terms are irrational.
Remarks. An example of a geometric progression with three rational and two irrational numbers is given - 3 points. It is proven that there cannot be more than three rational numbers, but no example is provided - 3 points. If both are present, 7 points.
|
3
|
Algebra
|
olympiads
| null | null |
\(\boxed{3}\)
|
Problem 8.1. In a box, there are oranges, pears, and apples, a total of 60 fruits. It is known that there are 3 times more apples than non-apples, and there are 5 times fewer pears than non-pears. How many oranges are in the box?
|
Since there are 3 times more apples than non-apples, apples make up $\frac{3}{4}$ of the total number of fruits, i.e., there are $\frac{3}{4} \cdot 60=45$ apples. Since there are 5 times fewer pears than non-pears, pears make up $\frac{1}{6}$ of the total number of fruits, i.e., there are $\frac{1}{6} \cdot 60=10$ pears. Therefore, the total number of oranges is $60-45-10=5$.
|
5
|
Algebra
|
olympiads
| null | null |
\(\boxed{5}\)
|
Problem 8.2. Oleg bought a chocolate bar for $n$ rubles, and after some time, he sold it for 96 rubles. It turned out that he sold the chocolate bar for exactly $n \%$ more than he bought it for. For how many rubles did Oleg buy the chocolate bar?
|
From the condition of the problem, it follows that $96=n \cdot\left(1+\frac{n}{100}\right)$. Transforming this equation, we get
$$
0=n^{2}+100 n-9600 \quad \Leftrightarrow \quad 0=(n+160)(n-60)
$$
Thus, $n=60$, since the chocolate bar cannot cost a negative number of rubles.
|
60
|
Algebra
|
olympiads
| null | null |
\(\boxed{60}\)
|
Problem 3.5. Vanya wrote the number 1347 on the board.
- Look! - noticed Petya. - In this number, each of the last two digits is equal to the sum of the two preceding ones.
- Exactly! - agreed Vasya.
- Can you write the largest four-digit number like this?
Help Vasya complete Petya's task.
|
It is clear that in the number 9099, each of the two last digits is equal to the sum of the two preceding ones.
If there existed a four-digit number with such a property that was even larger, then its first digit would be 9, and the second digit would be no less than 1. But then the third digit would be no less than $9+1=10$, which is impossible.
|
9099
|
Number Theory
|
olympiads
| null | null |
\(\boxed{9099}\)
|
Problem 3.6. Petya can draw only 4 things: the sun, a ball, a tomato, and a banana. But he does it extremely realistically! Today he drew several things, among which there were exactly 15 yellow, 18 round, and 13 edible. What is the maximum number of balls he could have drawn?
Petya believes that all tomatoes are round and red, all balls are round and can be of any color, and all bananas are yellow and not round.
|
Since there are a total of 18 round objects, and all balls are round, there were no more than 18 balls. Note that there could have been exactly 18, if 2 yellow balls, 16 green balls, and 13 bananas were drawn.
|
18
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{18}\)
|
.1. Assign each letter a digit $1,2,3,4,5$ so that all inequalities are satisfied.
$$
3>\mathrm{A}>\mathrm{M}<\mathrm{E}<\mathrm{H}<\mathrm{A}
$$
Different letters must correspond to different digits. Write the number ZAMENA as your answer.
|
From the condition, it follows that $\mathrm{M}<\mathrm{E}<\mathrm{H}<\mathrm{A}<3$. The numbers from 1 to 5 are uniquely ordered, so $\mathrm{M}=1, \mathrm{E}=2, \mathrm{H}=3, \mathrm{~A}=4,3=5$. Then ZAMENA $=541234$.
|
541234
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{541234}\)
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.