problem
stringlengths 17
4.31k
| solution_hint
stringlengths 49
6.77k
| answer
stringlengths 1
44
⌀ | problem_type
stringclasses 8
values | source
stringclasses 2
values | level
stringclasses 3
values | type
stringclasses 7
values | solution
stringlengths 13
56
|
|---|---|---|---|---|---|---|---|
.2. Find the smallest number in which all digits are different, and the sum of all digits is 32.
|
For a four-digit number with different digits, the maximum possible sum of digits is $9+8+7+6=30<32$, so the number we need must be at least five digits.
We will try to make the first digit as small as possible. It is clear that it is no less than 2. We will place 2 in the first position. The sum of the remaining four digits is 30, which can only be obtained as $9+8+7+6$. We place the smallest of these digits, 6, in the second position, the next largest digit, 7, in the third position, 8 in the fourth, and 9 in the fifth.
|
26789
|
Number Theory
|
olympiads
| null | null |
\(\boxed{26789}\)
|
# 011011010011.
Information has emerged that this encoding has been deciphered, as a result of which the agent will have to use a backup encoding. In it, the letter A is replaced by 21, the letter B by 122, and the letter V by 1. What code will this message receive in the new encoding?
|
Let's look at the right end of the code. Two ones at the end can only come from the letter A: 011011010011.
Next, we look at the rightmost digit of those we haven't figured out yet, from which letter it came. The digit 0 at the end is only present in B: 011011010011.
Similarly, the previous letter is also B: 011011010011.
Now the "undeciphered" rightmost digit is 1. Before it stands a 0. This can only come from the letter B: 011011010011.
The "undeciphered" digits on the right are two ones. This can only come from A:
The message obtained is ABBBA, which when encoded anew gives 211221121.
A B BB A
|
211221121
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{211221121}\)
|
Problem 5.2. Several people were seated around a round table such that the distances between adjacent people are the same. One of them was given a sign with the number 1, and then everyone was given signs with numbers 2, 3, and so on, in a clockwise direction.
The person with the sign numbered 31 noticed that the distance from them to the person with the sign numbered 7 is the same as the distance to the person with the sign numbered 14. How many people in total sat at the table?
|
For such a situation to be possible, people from the 31st to the 14th need to be counted in a circle in the direction of decreasing numbers, and from the 31st to the 7th - in a circle in the direction of increasing numbers.
There are 16 people sitting between the 31st and the 14th. Therefore, there are also 16 people between the 31st and the 7th. Among them, 6 have numbers from 1 to 6, so the remaining $16-6=10$ people are those with numbers from the 32nd. The largest number is 41.
|
41
|
Number Theory
|
olympiads
| null | null |
\(\boxed{41}\)
|
Problem 6.1. Five consecutive natural numbers are written in a row. The sum of the three smallest of them is 60. What is the sum of the three largest?
|
The fifth number is 4 more than the first, and the fourth is 2 more than the second. Then the sum of the three largest numbers is $2+4=6$ more than the sum of the three smallest, and it is equal to $60+6=66$.
|
66
|
Algebra
|
olympiads
| null | null |
\(\boxed{66}\)
|
Problem 7.1. Sasha and Vanya are playing a game. Sasha asks Vanya questions. If Vanya answers correctly, Sasha gives him 7 candies. If Vanya answers incorrectly, he gives Sasha 3 candies. After Sasha asked 50 questions, it turned out that each of them had as many candies as they had at the beginning. How many questions did Vanya answer correctly?
|
Let Vanya answer correctly to $x$ questions, then he answered incorrectly to $50-x$ questions. This means that during the game, Vanya received $7 x$ candies and gave away $3(50-x)$ candies. Since the total number of candies for both boys did not change after the game, we get $7 x=3(50-x)$. Solving this, we find $x=15$.
Remark. The same answer could have been obtained by understanding that to "balance the candies," Vanya should "compensate" every 3 correct answers with 7 incorrect ones.
|
15
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{15}\)
|
Problem 7.3. Numbers were placed in the cells of a square such that the sums of the numbers in each vertical, horizontal, and each diagonal of three cells are equal. Then some numbers were hidden. What is the sum of the numbers in the two shaded cells?
| 16 | | |
| :--- | :--- | :--- |
| | | 10 |
| 8 | | 12 |
|
Let $a$ be the number in the top right cell, and $b$ be the number in the central cell. The sum of the diagonal containing the number 8 and the sum of the numbers in the right column have a common term $a$, so $8+b=10+12$, from which $b=14$. The sums of the three numbers along both diagonals have a common number $b$, so $16+12=8+a$, from which $a=20$. Therefore, $a+b=20+14=34$.
Remark. The other numbers can also be placed to verify that the problem's condition is correct:
| 16 | 6 | 20 |
| :---: | :---: | :---: |
| 18 | 14 | 10 |
| 8 | 22 | 12 |
|
34
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{34}\)
|
Problem 7.4. Masha and Olya bought many identical pens for the new school year at the store. It is known that one pen costs an integer number of rubles, more than 10. Masha bought pens for exactly 357 rubles, and Olya - for exactly 441 rubles. How many pens did they buy in total?
|
Let the pen cost $r$ rubles. Then the numbers 357 and 441 are divisible by $d$. Since the greatest common divisor of the numbers $357=3 \cdot 7 \cdot 17$ and $441=3^{2} \cdot 7^{2}$ is $3 \cdot 7$, then 21 is also divisible by $r$. Since $r>10$, then $r=21$. Therefore, the total number of pens bought is $\frac{357}{21}+\frac{441}{21}=17+21=38$.
|
38
|
Number Theory
|
olympiads
| null | null |
\(\boxed{38}\)
|
Problem 7.7. The numbers from 1 to 200 were arranged in a random order on a circle such that the distances between adjacent numbers on the circle are the same.
For any number, the following is true: if you consider 99 numbers standing clockwise from it and 99 numbers standing counterclockwise from it, there will be an equal number of numbers that are smaller than it in both groups. Which number stands opposite the number 113?
|
Consider the number 2. Less than it is only the number 1. Since it is unique, it cannot be in any of the groups relative to the number 2. Therefore, 1 must be opposite 2.
Consider the number 4. The numbers less than it are three in number - an odd count. This means that one of them should not be in any of the groups relative to the number 4, i.e., it should be opposite. Since 1 and 2 are already standing opposite each other, 3 is opposite 4.
Continuing similar reasoning further, we get that opposite any even number stands an odd number that is one less than it. Thus, opposite the number 114 stands the number 113. And vice versa: opposite 113 stands 114.
|
114
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{114}\)
|
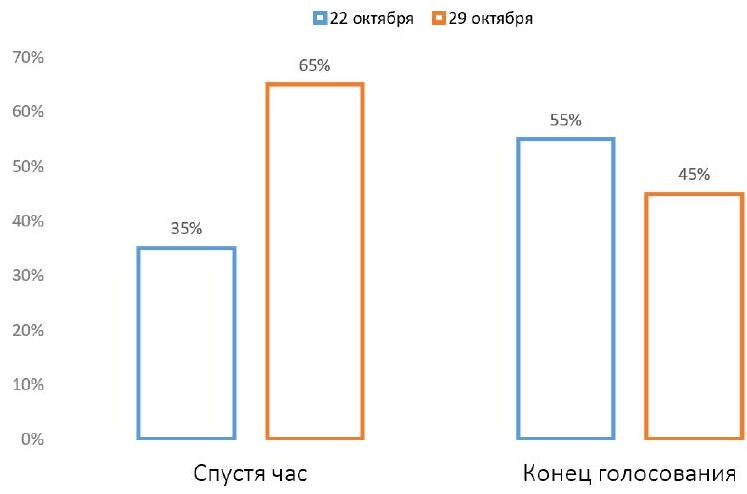
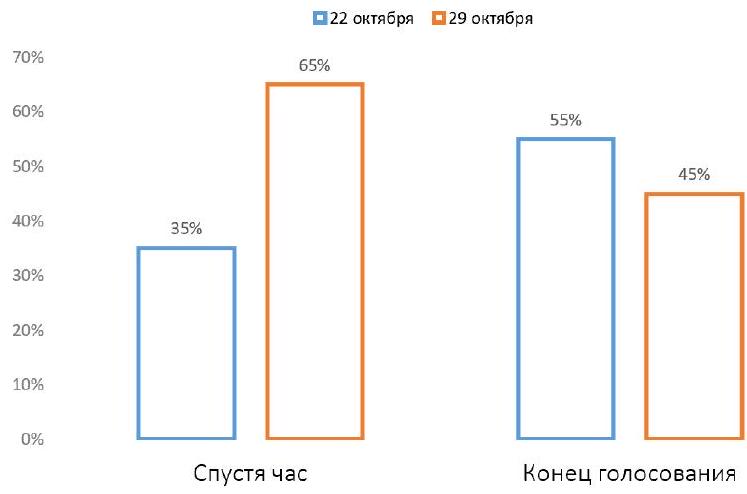
Problem 8.2. In the chat of students from one of the schools, a vote was held: "On which day to hold the disco: October 22 or October 29?"
The graph shows how the votes were distributed an hour after the start of the voting.
Then, 80 more people participated in the voting, voting only for October 22. After that, the voting ended. The final distribution of votes is also shown on the graph.
How many people participated in the voting?
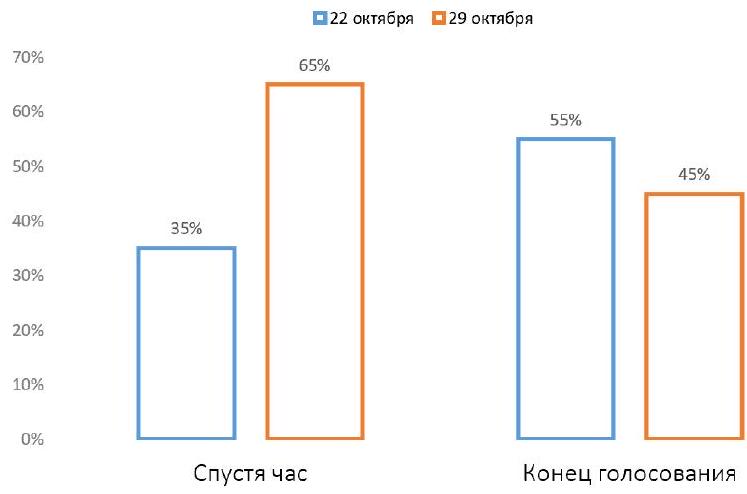
|
Let $x$ be the number of people who voted an hour after the start. From the left chart, it is clear that $0.35 x$ people voted for October 22, and $-0.65 x$ people voted for October 29.
In total, $x+80$ people voted, of which $45\%$ voted for October 29. Since there are still $0.65 x$ of them, we get the equation
$0.65 x=0.45(x+80)$, from which we find $x=180$. Therefore, a total of $180+80=260$ people participated in the voting.
|
260
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{260}\)
|
Problem 8.5. The numbers $1, 2, 3, \ldots, 235$ were written on a board. Petya erased some of them. It turned out that among the remaining numbers, no number is divisible by the difference of any two others. What is the maximum number of numbers that could remain on the board?
|
odd numbers could remain on the board: none of them is divisible by the difference of any two others, because this difference is even.
Suppose at least 119 numbers could remain. Consider 118 sets: 117 pairs $(1,2)$, $(3,4),(5,6), \ldots,(233,234)$ and one number 235. By the Pigeonhole Principle, in one of these sets, at least two numbers remained. This means that among the remaining numbers, there will be two consecutive numbers, but then their difference, equal to 1, is a divisor of any other remaining number. Contradiction.
|
118
|
Number Theory
|
olympiads
| null | null |
\(\boxed{118}\)
|
Problem 9.1. On an island, there live red, yellow, green, and blue chameleons.
- On a cloudy day, either one red chameleon changes its color to yellow, or one green chameleon changes its color to blue.
- On a sunny day, either one red chameleon changes its color to green, or one yellow chameleon changes its color to blue.
In September, there were 18 sunny and 12 cloudy days. As a result, the number of yellow chameleons increased by 5. By how much did the number of green chameleons increase?
|
Let $A$ be the number of green chameleons on the island, and $B$ be the number of yellow chameleons. Consider the quantity $A-B$. Note that each cloudy day it decreases by 1, and each sunny day it increases by 1. Since there were $18-12=6$ more sunny days than cloudy days in September, the quantity $A-B$ increased by 6 over this period. Since $B$ increased by 5, $A$ must have increased by $5+6=11$.
|
11
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{11}\)
|
Problem 9.2. Denis has cards with numbers from 1 to 50. How many ways are there to choose two cards such that the difference between the numbers on the cards is 11, and the product is divisible by 5?
The order of the selected cards does not matter: for example, the way to choose cards with numbers 5 and 16, and the way to choose cards with numbers 16 and 5 - this is the same way.
|
For the product to be divisible by 5, it is necessary and sufficient that one of the factors is divisible by 5. Let $n$ be the chosen number divisible by 5, then its pair should be $n-11$ or $n+11$, and both chosen numbers must be natural numbers. Clearly, for $n=5,10,40,45,50$ there is only one way to choose a pair, while for $n=15,20,25,30,35$ there are exactly two ways to choose a pair. In total, $5 \cdot 1+5 \cdot 2=15$ ways.
|
15
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{15}\)
|
Problem 9.3. Traders Andrey and Boris bought 60 bags of potatoes each from the same farmer. All the bags cost the same.
Andrey sold all his bags, increasing their price by $100 \%$. Boris first increased the price by $60 \%$, and after selling 15 bags, increased the price by another $40 \%$ and sold the remaining 45 bags.
It turned out that Boris earned 1200 rubles more than Andrey. How many rubles did one bag of potatoes cost from the farmer?
|
Let the bag cost the farmer $x$ rubles. Andrei and Boris spent the same amount on buying 60 bags.
From the condition, it follows that Andrei sold 60 bags for $2 x$ rubles each, i.e., he received $60 \cdot 2 x$ rubles. Boris, on the other hand, sold 15 bags at a price of $1.6 x$ rubles and then sold 45 bags at a price of $1.6 x \cdot 1.4$ rubles. We get the equation
$$
2 x \cdot 60 + 1200 = 15 \cdot 1.6 x + 45 \cdot 1.6 x \cdot 1.4
$$
Solving it, we find $x=250$.
|
250
|
Algebra
|
olympiads
| null | null |
\(\boxed{250}\)
|
.1. Find the largest 12-digit number $N$ that satisfies the following two conditions:
- In the decimal representation of the number $N$, there are six digits «4» and six digits «7»;
- In the decimal representation of the number $N$, no four consecutive digits form the number «7444».
|
It is clear that the number 777744744744 meets the condition of the problem.
Suppose there exists a larger number, then it must start with four sevens. In this number, we select the largest number of consecutive fours, let there be $k$ of them. If $k \geqslant 3$, then by selecting among these $k$ fours the three leftmost ones, as well as the seven to the left of them, we get a segment of digits "7444," which is a contradiction.
Therefore, $k \leqslant 2$. In the last eight digits of the number, there must be six fours. Since no three consecutive digits can all be fours, the last eight digits are uniquely determined: they are 44744744. But the corresponding number 777744744744 we have already found.
|
777744744744
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{777744744744}\)
|
.1. The product of nine consecutive natural numbers is divisible by 1111. What is the smallest possible value that the arithmetic mean of these nine numbers can take?
|
Let these nine numbers be $-n, n+1, \ldots, n+8$ for some natural number $n$. It is clear that their arithmetic mean is $n+4$.
For the product to be divisible by $1111=11 \cdot 101$, it is necessary and sufficient that at least one of the factors is divisible by 11, and at least one of the factors is divisible by 101. Therefore, one of the nine numbers must be at least 101, so $n+8 \geqslant 101$ and $n+4 \geqslant 97$. It is also clear that for the nine numbers $93,94, \ldots, 101$, the value $n+4=97$ is achieved, since 99 is divisible by 11, and 101 is divisible by 101.
|
97
|
Number Theory
|
olympiads
| null | null |
\(\boxed{97}\)
|
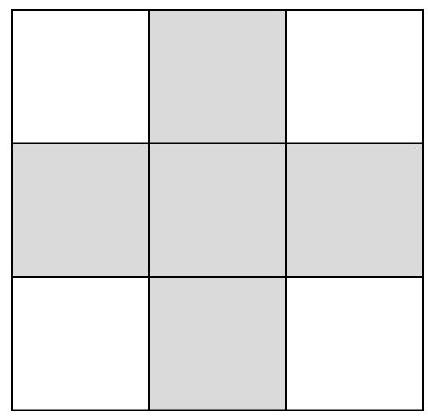
Problem 8.2. The numbers from 1 to 9 were placed in the cells of a $3 \times 3$ table such that the sum of the numbers on one diagonal is 7, and on the other - 21. What is the sum of the numbers in the five shaded cells?
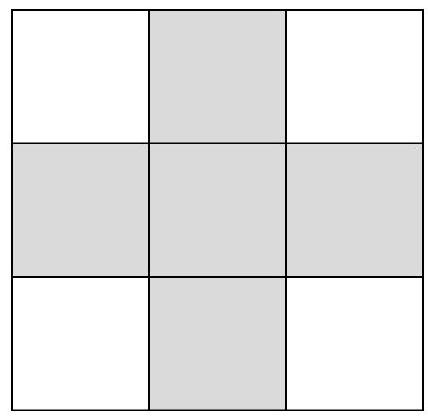
|
Note that 7 can be represented uniquely as the sum of numbers from 1 to 9 - this is $1+2+4=7$.
Let's look at the other diagonal with a sum of 21. The largest possible value of the sum in it is $9+8+4=21$ (since the number in the central cell is no more than 4). Therefore, it must contain the numbers $9,8,4$.
Thus, the number 4 is in the central cell, and the numbers 1, 2, 8, and 9 are at the corners. Now it is not difficult to find the sum of the numbers in the shaded cells: $3+4+5+6+7=25$.
|
25
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{25}\)
|
1. Variant 1.
Find the sum:
$$
(-2021)+(-2020)+(-2019)+\ldots+2023+2024
$$
|
By pairing numbers that differ in sign, we get that in each such pair the sum is 0, and without pairs, the numbers left are $0, 2022, 2023, 2024$.
|
6069
|
Algebra
|
olympiads
| null | null |
\(\boxed{6069}\)
|
# 3. Option 1.
In the village, 7 people live. Some of them are liars who always lie, while the rest are knights (who always tell the truth). Each resident said whether each of the others is a knight or a liar. A total of 42 answers were received, and in 24 cases, a resident called a fellow villager a liar. What is the minimum number of knights that can live in the village?
|
The phrase "He is a knight" would be said by a knight about a knight and by a liar about a liar, while the phrase "He is a liar" would be said by a knight about a liar and by a liar about a knight. Therefore, in each pair of "knight-liar," the phrase "He is a liar" will be said twice. Since this phrase was said 24 times in total, there are 12 pairs of "knight-liar," from which we can determine that there are 3 knights and 4 liars, or vice versa.
|
3
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{3}\)
|
# 6. Variant 1.
What is the largest root that the equation
$$
(x-a)(x-b)=(x-c)(x-d)
$$
can have if it is known that $a+d=b+c=2022$, and the numbers $a$ and $c$ are different?
|
By expanding the brackets and combining like terms, we find $x=\frac{c d-a b}{c+d-a-b}$. Note that $c+d-a-b \neq 0$, because otherwise $c+d=a+b$, and considering the equality $a+d=b+c$, we would get $a=c$.
Considering that $d=2022-a, c=2022-b, x=\frac{2022^{2}-2022 a-2022 b}{2(2022-a-b)}=\frac{2022}{2}=1011$.
|
1011
|
Algebra
|
olympiads
| null | null |
\(\boxed{1011}\)
|
Task No. 1.1
## Condition:
Five friends - Masha, Nastya, Irina, Olya, and Anya - meet in the park every day after buying ice cream from the shop around the corner. One day, the girls had a conversation.
Irina: I was the first in line!
Olya: No one was after me.
Anya: Only one person was after me.
Masha: There were five people in front of me.
Nastya: I was standing next to Irina.
The girls are friends, so they don't lie to each other. How many people were between Masha and Nastya?
|
Exact match of the answer - 1 point
## Solution.
From the statements of Irina and Olya, it is clear that they were first and last, respectively. Since there was only one person after Anya, it was Olya. Nastya stood next to Irina, but she could not have stood in front of her, so Nastya was second. This means that Masha stood somewhere between Nastya and Anya, and since there were five people in front of her, two of whom were Irina and Nastya, there were exactly three people between Masha and Nastya.
|
3
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{3}\)
|
# Task № 2.1
## Condition:
Karlson and Little together weigh 10 kg more than Freken Bok, and Little and Freken Bok weigh 30 kg more than Karlson. How much does Little weigh? Give your answer in kilograms.
|
Exact match of the answer -1 point
Solution.
Let's denote Carlson's mass by K, Freken Bok's mass by F, and Little One's mass by M. Then from the condition, it follows that $K+M=F+10$ and $M+F=K+30$. Adding these equations term by term, we get $K+2M+F=F+K+40$. From this, $M=20$.
|
20
|
Algebra
|
olympiads
| null | null |
\(\boxed{20}\)
|
# Task № 5.1
## Condition:
Polina thought of a natural number. Her friends asked one question each:
Masha: Is it divisible by 11?
Irina: Is it divisible by 13?
Anya: Is it less than 15?
Olya: Is it divisible by 143?
Polina answered affirmatively to only two of the four questions. What numbers could Polina have thought of? List all possible options.
## Answers:
$\circ 11$
$\circ 13$
## Exact match of the answer - 1 point
|
If Olya were right, the number would be divisible by 143, but in that case, it would also be divisible by 11 and 13, which means there would be at least three affirmative answers. Therefore, the number is not divisible by 143. If both Masha and Irina were right, the number would be divisible by both 11 and 13, but in that case, it would also be divisible by 143, which we have already determined is not the case. Therefore, at most one of Masha's and Irina's answers could be affirmative. In order for there to be two affirmative answers, Anya must be right, and one of Masha and Irina must be wrong. This means there are two possibilities: either Masha and Anya are right, or Irina and Anya are right. In the first case, the answer is 11, and in the second case, it is 13.
|
1113
|
Number Theory
|
olympiads
| null | null |
\(\boxed{1113}\)
|
Problem 7.1. Denis thought of four different natural numbers. He claims that
- the product of the smallest and the largest numbers is 32;
- the product of the two remaining numbers is 14.
What is the sum of all four numbers?
|
There are two ways to represent the number 14 as the product of two numbers: $1 \cdot 14$ and $2 \cdot 7$; therefore, the second and third largest numbers are 1 and 14 or 2 and 7. The first case does not work for us, as 1 cannot be the second largest number. So, the second largest number is 2, and the third largest is 7.
Since our four numbers are distinct, the smallest (first by size) number is 1. Then the largest number is 32. From this, it is not difficult to find the sum of all the numbers.
|
42
|
Number Theory
|
olympiads
| null | null |
\(\boxed{42}\)
|
Problem 7.5. At a tribal council meeting, 60 people spoke in turn. Each of them said only one phrase. The first three speakers said the same thing: "I always tell the truth!" The next 57 speakers also said the same phrase: "Among the previous three speakers, exactly two told the truth." What is the maximum number of speakers who could have told the truth?
|
Note that among any four consecutive speakers, at least one lied (if the first three told the truth, then the fourth definitely lied). By dividing 60 people into 15 groups of four consecutive speakers, we get that at least 15 people lied, meaning no more than 45 people told the truth.
To construct an example, assume that the first three in each group of four (in the above division) tell the truth, while the fourth lies. It is easy to see that this situation meets the condition.
|
45
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{45}\)
|
Problem 7.7. In the classroom, there are several single desks (no more than one person can sit at each desk; there are no other desks in the classroom). During the break, a quarter of the students went out into the corridor, and the number of people left in the classroom was equal to 4/7 of the total number of desks. How many desks are in the room if there are no more than 30?
|
Note that the number of remaining students is $\frac{3}{4}$ of the initial number, so it must be divisible by 3. Let's denote it by $3x$. Let $y$ be the number of desks. Then
$$
3 x=\frac{4}{7} y
$$
from which $21 x=4 y$. Since 4 and 21 are coprime, $y$ must be divisible by 21. From the problem's condition, we know that $y \leqslant 30$, so $y=21$.
|
21
|
Algebra
|
olympiads
| null | null |
\(\boxed{21}\)
|
Problem 7.8. Tanya and Vера are playing a game. Tanya has cards with numbers from 1 to 30. She arranges them in some order in a circle. For each pair of adjacent numbers, Vера calculates their difference, subtracting the smaller number from the larger one, and writes down the resulting 30 numbers in her notebook. After that, Vера gives Tanya a number of candies equal to the smallest number written in the notebook. Tanya arranges the cards so as to get as many candies as possible. What is the maximum number of candies she can get?
|
We will prove that Tanya cannot get 15 candies. Let's look at the card with the number 15. The number 15 differs from all the remaining numbers, except for the number 30, by no more than 14. Thus, at least one of the differences involving the number 15 will be no more than 14.
Let's provide an example of an arrangement where Tanya can get 14 candies. Arrange the numbers in a circle in the following order: $1,16,2,17,3,18, \ldots, 14,29,15,30$.
|
14
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{14}\)
|
11.1 From a three-digit number $A$, which does not contain zeros in its notation, a two-digit number $B$ was obtained by writing the sum of the first two digits instead of them (for example, the number 243 turns into 63). Find $A$ if it is known that $A=3 B$.
|
The last digit of the numbers $B$ and $A=3B$ is the same, so this digit is 5. Moreover, $A$ is divisible by 3, which means $B$ is also divisible by 3 (the sums of the digits are the same). Therefore, $B$ is one of the numbers $15, 45, 75$. By checking, we find that the number $B=45$ satisfies the condition.
Comment: A correct answer without justification - 2 points.
|
135
|
Number Theory
|
olympiads
| null | null |
\(\boxed{135}\)
|
3.1. A pedestrian left point $A$ for point $B$. At the same time, a cyclist left point $B$ for point $A$. After one hour, the pedestrian was three times farther from the cyclist than from point $A$. Another 30 minutes later, they met, after which both continued their journey. How many hours did it take the pedestrian to travel from $A$ to $B$?
|
Let the distance from $A$ to $B$ be 1 km, the pedestrian moves at a speed of $x$ km/h, and the cyclist at $y$ km/h. Then in one hour, the pedestrian has walked $x$ km, the cyclist has traveled $y$ km, and the distance between them is $1-x-y$, which should be three times $x$. Therefore, $3 x=1-x-y, y=1-4 x$. In the next half hour, they will together cover $1-x-y$ km. Since their closing speed is $x+y$, we get the equation $\frac{1}{2}(x+y)=1-x-y$, from which $x+y=\frac{2}{3}$. Substituting $y=1-4 x$ into the last equation: $1-3 x=\frac{2}{3}, x=\frac{1}{9}$. Therefore, it will take the pedestrian 9 hours to travel the distance from $A$ to $B$.
|
9
|
Algebra
|
olympiads
| null | null |
\(\boxed{9}\)
|
5.1. How many six-digit numbers exist that consist only of the digits 1 and 2, given that each of them appears?
|
There are a total of $64=2^{6}$ six-digit numbers consisting of the digits 1 and 2, since there are 6 positions and for each position, there are two options to place a digit. However, two numbers - the one consisting only of ones and the one consisting only of twos - do not satisfy the condition, so 62 numbers remain.
|
62
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{62}\)
|
6.1. Coins come in denominations of 50 kopecks, 1 ruble, 2 rubles, 5 rubles, 10 rubles. $V$ has several coins in his wallet. It is known that no matter which 20 coins are taken out of the wallet, there will be at least one 1-ruble coin, at least one 2-ruble coin, and at least one 5-ruble coin. What is the maximum number of coins in the wallet for this to be possible?
|
Example: 9 coins of 1 ruble, 9 coins of 2 rubles, 9 coins of 5 rubles, and 1 coin of 10 rubles. Note that the wallet contains a total of $9+9+1=19$ coins that are not 1 ruble, so among any 20 coins, there will definitely be a 1-ruble coin. Similarly, this can be verified for all other denominations.
Estimate: Suppose there are $x$ coins in the wallet. Since the number of coins not worth 1 ruble is no more than 19 (otherwise, there would be 20 coins without a 1-ruble coin), the number of 1-ruble coins must be at least $x-19$. Similarly for 2-ruble and 5-ruble coins. Therefore, the total number of coins is at least $3(x-19)$. We get the inequality $x \geqslant 3 x-57$, from which $57 \geqslant 2 x, 28.5 \geqslant x$. Since $x$ is an integer, it does not exceed 28.
|
28
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{28}\)
|
7.1. In a football tournament, 20 teams participated. Each team played one match against each other. A team receives 3 points for a win, 1 point for a draw, and 0 points for a loss. After the tournament, Vasya calculated the total points scored by the teams. It turned out to be 500. How many matches ended in a draw?
|
Each team played 19 matches, so the total number of matches played was $20 \cdot 19 / 2=190$ (we divide by two because each match is counted twice). If there were no draws, the total points would be $3 \cdot 190=570$. Each draw results in one point less in the total compared to a match that ends with one team winning (the total points scored is 2, not 3). Since we need to reduce the total by 70 points, there must be 70 draws.
|
70
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{70}\)
|
8.1. The real number a is such that $2a - 1/a = 3$. What is the value of $16a^4 + 1/a^4$?
|
Squaring the equality from the condition, we get $4 a^{2}-4+1 / a^{2}=9$, that is, $4 a^{2}+1 / a^{2}=13$. Squaring again, we obtain $16 a^{4}+8+1 / a^{4}=169$. Therefore, $16 a^{4}+1 / a^{4}=161$.
|
161
|
Algebra
|
olympiads
| null | null |
\(\boxed{161}\)
|
8-2. On a distant planet in the mangrove forests, there lives a population of frogs. The number of frogs born each year is one more than the difference between the number of frogs born in the previous two years (the larger number minus the smaller number).
For example, if 5 frogs were born last year and 2 in the year before, then 4 frogs will be born this year; if 3 frogs were born last year and 10 in the year before, then 8 frogs will be born this year.
In 2020, 2 frogs were born, and in 2021, 9. In which nearest year will only 1 frog be born for the first time?
|
This is a fairly simple problem where the only thing you need to do is correctly understand the condition and apply it the necessary number of times. The ability to correctly understand the condition is an important skill in solving problems!
By applying the algorithm described in the condition, we get that the number of frogs born on the planet is $2 \rightarrow 9 \rightarrow 8 \rightarrow 2 \rightarrow 7 \rightarrow 6 \rightarrow 2 \rightarrow 5 \rightarrow 4 \rightarrow 2 \rightarrow 3 \rightarrow 2 \rightarrow 2 \rightarrow 1$, which means that 12 more years need to pass starting from 2021, hence the answer is 2033.
|
2033
|
Other
|
olympiads
| null | null |
\(\boxed{2033}\)
|
Problem 4.3. How many rectangles exist on this picture with sides running along the grid lines? (A square is also a rectangle.)
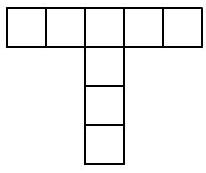
|
In a horizontal strip $1 \times 5$, there are 1 five-cell, 2 four-cell, 3 three-cell, 4 two-cell, and 5 one-cell rectangles. In total, $1+2+3+4+5=15$ rectangles.
In a vertical strip $1 \times 4$, there are 1 four-cell, 2 three-cell, 3 two-cell, and 4 one-cell rectangles. In total, $1+2+3+4=10$ rectangles. At the same time, one one-cell rectangle at the intersection of the strips is counted twice (and only it is). Therefore, the answer to the problem is the number $15+10-1=24$.
|
24
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{24}\)
|
Problem 5.3. A cuckoo clock is hanging on the wall. When a new hour begins, the cuckoo says "cuckoo" a number of times equal to the number the hour hand points to (for example, at 19:00, "cuckoo" sounds 7 times). One morning, Maxim approached the clock when it was 9:05. He started turning the minute hand until he advanced the clock by 7 hours. How many times did "cuckoo" sound during this time?

|
The cuckoo will say "cuckoo" from 9:05 to 16:05. At 10:00 it will say "cuckoo" 10 times, at 11:00 - 11 times, at 12:00 - 12 times. At 13:00 (when the hand points to the number 1) "cuckoo" will sound 1 time. Similarly, at 14:00 - 2 times, at 15:00 - 3 times, at 16:00 - 4 times. In total
$$
10+11+12+1+2+3+4=43
$$
|
43
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{43}\)
|
Problem 7.7. In three of the six circles of the diagram, the numbers 4, 14, and 6 are recorded. In how many ways can natural numbers be placed in the remaining three circles so that the products of the triples of numbers along each of the three sides of the triangular diagram are the same?
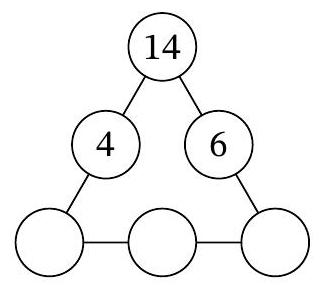
|
Let $a, b, c$ be the natural numbers in the three lower circles, from left to right. According to the condition, $14 \cdot 4 \cdot a = 14 \cdot 6 \cdot c$, i.e., $2a = 3c$. From this, it follows that $3c$ is even, and therefore $c$ is even. Thus, $c = 2k$ for some natural number $k$, and from the equation $2a = 3c$ it follows that $a = 3k$.
It must also hold that $14 \cdot 4 \cdot 3k = 3k \cdot b \cdot 2k$, which means $b \cdot k = 28$. Note that by choosing the number $k$, which is a natural divisor of 28, the natural numbers $a, b, c$ are uniquely determined. The number 28 has exactly 6 natural divisors: $1, 2, 4, 7, 14, 28$. Therefore, there are also 6 ways to place the numbers in the circles.
|
6
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{6}\)
|
10.2. Solve the equation:
$1+\frac{3}{x+3}\left(1+\frac{2}{x+2}\left(1+\frac{1}{x+1}\right)\right)=x$.
|
# Solution.
$1+\frac{1}{x+1}=\frac{x+2}{x+1}$, therefore the given equation is equivalent to the equation $1+\frac{3}{x+3}\left(1+\frac{2}{x+1}\right)=x$ under the condition that $\mathrm{x} \neq-2$. Proceeding similarly, we get $1+\frac{3}{x+3}=x$, where $\mathrm{x} \neq-2$ and $\mathrm{x} \neq-3$. The roots of this equation are the numbers 2 and -2, so the only root of the original equation is the number 2.
## Grading Criteria
- Only the correct answer is provided - 1 point.
- The correct solution process, but the extraneous root is not discarded - 3 points.
|
2
|
Algebra
|
olympiads
| null | null |
\(\boxed{2}\)
|
1. Variant 1.
When multiplying a two-digit and a three-digit number, a four-digit number of the form $A=\overline{a b a b}$ is obtained. Find the largest $A$, given that $A$ is divisible by 14.
|
Note that $A=\overline{a b a b}=\overline{a b} \cdot 101$. Since 101 and 14 are coprime, $\overline{a b}$ is divisible by 14. The maximum value of $\overline{a b}=98$.
|
9898
|
Number Theory
|
olympiads
| null | null |
\(\boxed{9898}\)
|
2. Variant 1. Find the number of four-digit numbers where the digit in the units place is exactly 1 more than the digit in the tens place (the number cannot start with zero).
|
The leading digit of the number can be chosen in 9 ways (any digit except zero). The digit in the hundreds place can be chosen in 10 ways (any digit will do). The digit in the tens place can be any digit from 0 to 8, and the digit in the units place is uniquely determined by the chosen digit in the tens place. In total, there are $9 \cdot 10 \cdot 9=810$ options.
|
810
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{810}\)
|
3. Option 1.
In the Ivanov family, both the mother and the father, and their three children, were born on April 1st. When the first child was born, the parents' combined age was 45 years. The third child in the family was born a year ago, when the sum of the ages of all family members was 70 years. How old is the middle child now, if the sum of the ages of the children is 14 years?
|
If the first child is older than the second child by $x$ years, and the middle child is older than the third child by $y$ years, then $70-45=3(x+y)+y$, because the age of each parent and the eldest child increased by $(x+y)$ years by the time the third child was born, and the age of the second child increased by $y$ years. Similarly, $(x+y+1)+(y+1)+1=14$. We have the system of equations $3x+4y=25, x+2y=11$, from which we find $x=3, y=4$.
|
5
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{5}\)
|
7. Variant 1.
Numbers $x$ and $y$ satisfy the equation $\frac{x}{x+y}+\frac{y}{2(x-y)}=1$. Find all possible values of the expression $\frac{5 x+y}{x-2 y}$, and in the answer, write their sum.
|
By bringing to a common denominator and combining like terms, we get the equality $3 y^{2}=x y$. If $y=0$, then $x$ is any non-zero number. In this case, the value of the expression is 5. If $x=3 y \neq 0$, then in this case, the value of the expression is 16. The final answer is $5+16=21$.
|
21
|
Algebra
|
olympiads
| null | null |
\(\boxed{21}\)
|
# 8. Variant 1.
Consider the quadratic trinomial $P(x)=a x^{2}+b x+c$, which has distinct positive roots. Vasya wrote four numbers on the board: the roots of $P(x)$, as well as the roots of the trinomial $Q(x)=c x^{2}+b x+a$ multiplied by 4. What is the smallest integer value that the sum of the written numbers can have
|
Let the roots of the quadratic polynomial $P(x)$ be $x_{1}, x_{2}>0$. Then, by Vieta's formulas, the roots of the polynomial $Q(x)$ will be $\frac{1}{x_{1}}, \frac{1}{x_{2}}$.
The sum of the numbers written on the board is $S=x_{1}+x_{2}+\frac{4}{x_{1}}+\frac{4}{x_{2}}$. For a positive $k$, the inequality $k+\frac{4}{k} \geq 4$ holds, and equality is achieved if and only if $k=2$.
Therefore, $S \geq 8$. However, $S=8$ only if $x_{1}=x_{2}=2$. But according to the problem, $x_{1}, x_{2}$ are distinct. Therefore, $S>8$. Thus, the smallest possible integer value of $S$ is 9. This situation is possible. Let $x_{1}=1$, and $x_{2}$ be such that $x_{2}+\frac{4}{x_{2}}=5$. Then the quadratic polynomial with roots $x_{1}, x_{2}$ is the desired one.
|
9
|
Algebra
|
olympiads
| null | null |
\(\boxed{9}\)
|
Problem 8.2. In the chat of students from one of the schools, a vote was held: "On which day to hold the disco: October 22 or October 29?"
The graph shows how the votes were distributed an hour after the start of the voting.
Then, 80 more people participated in the voting, voting only for October 22. After that, the voting ended. The final distribution of votes is also shown on the graph.
How many people participated in the voting?
|
Let $x$ be the number of people who voted an hour after the start. From the left chart, it is clear that $0.35 x$ people voted for October 22, and $-0.65 x$ people voted for October 29.
In total, $x+80$ people voted, of which $45\%$ voted for October 29. Since there are still $0.65 x$ of them, we get the equation
$0.65 x=0.45(x+80)$, from which we find $x=180$. Therefore, a total of $180+80=260$ people participated in the voting.
|
260
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{260}\)
|
2. The distance between points A and B is 90 km. At 9:00, a bus left point A for point B at a speed of 60 km/h. Starting from 9:00, every 15 minutes, buses leave point B towards point A at a speed of 80 km/h. The bus that left point A, after traveling 45 km, reduces its speed to 20 km/h due to a breakdown and continues at this speed. A passenger in this bus is considering whether to continue the slow journey to point B or return to point A in the first passing bus. How much time does the passenger have to make a decision?
|
A bus leaving point A will travel 45 km in $\frac{45}{60}$ hours. During this time, a bus leaving point B at 9:00 will travel $\frac{45}{60} \cdot 80=60$ km and will be closer to point A than the bus leaving point A. A bus leaving point B at 9:15 will travel $\left(\frac{45}{60}-\frac{15}{60}\right) \cdot 80=40$ km and will be 5 km away from the bus leaving point A. Therefore, the time it will take for them to meet is $\frac{5}{20+80}=\frac{1}{20}$ hours. The passenger has 3 minutes to make a decision.
|
3
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{3}\)
|
5. In the country, there are 20 cities. An airline wants to organize two-way flights between them so that from any city, it is possible to reach any other city with no more than $\mathrm{k}$ transfers. At the same time, the number of air routes should not exceed four. What is the smallest $\mathrm{k}$ for which this is possible?
|
$\mathrm{k}=2$. At least two transfers will be required. From an arbitrary city A, one can reach no more than four cities without a transfer, and with one transfer - no more than $4 \times 3=12$ cities. That is, if using no more than one transfer, one can fly to no more than 16 other cities, but 19 are required.
|
2
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{2}\)
|
1.1. On September 1, 2021, Vasya deposited 100,000 rubles in the bank. Exactly one year later, the bank accrues 10% annual interest (that is, it increases the amount by 10 percent of what was on the account at that moment, for example, on September 2, 2022, Vasya will have 110,000 rubles on his account). Find the smallest year number in which on September 2, the amount on Vasya's account will be more than 150,100 rubles.
|
Note that on September 2nd of the $(2021+n)$-th year, the account will have $100000 \cdot 1.1^{n}$ rubles. Since $100000 \cdot 1.1^{4}=146410<150100<161051=100000 \cdot 1.1^{5}$, the minimum $n$ for which the amount will exceed 150,100 rubles is 5. Therefore, the answer is: $2021+5=2026$.
|
2026
|
Algebra
|
olympiads
| null | null |
\(\boxed{2026}\)
|
3.1. Semyon was solving the quadratic equation $4 x^{2}+b x+c=0$ and found that its two roots are the numbers $\operatorname{tg} \alpha$ and $3 \operatorname{ctg} \alpha$ for some $\alpha$. Find $c$.
|
By Vieta's theorem, $c / 4$ equals the product of the roots. Considering that $\operatorname{tg} \alpha \cdot \operatorname{ctg} \alpha=1$, we get $c / 4=3$.
|
12
|
Algebra
|
olympiads
| null | null |
\(\boxed{12}\)
|
4.1. Given an arithmetic progression $a_{1}, a_{2}, \ldots, a_{100}$. It is known that $a_{3}=9.5$, and the common difference of the progression $d=0.6$. Find the sum $\left\{a_{1}\right\}+\left\{a_{2}\right\}+\ldots+\left\{a_{100}\right\}$. The notation $\{x\}$ represents the fractional part of the number $x$, i.e., the difference between $x$ and the greatest integer not exceeding $x$, for example: $\{4.7\}=0.7,\left\{-5 \frac{1}{3}\right\}=\frac{2}{3}$, etc.
|
Let's look at the first digits after the decimal point in the decimal representation of the terms of the progression. Since $d=0.6$ and $a_{3}=9.5$, the sequence of these digits is: $3,9,5,1,7,3,9,5,1,7, \ldots$ It is periodic with a period of 5. Then the sum of the fractional parts of any five consecutive terms in the progression is $0.3+0.9+0.5+0.1+0.7=2.5$. Therefore, the desired sum of the fractional parts is $20 \cdot 2.5=50$.
|
50
|
Algebra
|
olympiads
| null | null |
\(\boxed{50}\)
|
5.1. A random number sensor outputs a number $a$ - one of the natural numbers $1,2, \ldots, 100$ (with equal probability). For this value of $a$, we find the maximum possible value $M$ of the function
$$
f(x)=\frac{700}{x^{2}-2 x+2 a}
$$
The probability that $M>10$ is $n$ percent. What is $n$?
|
The minimum value of the quadratic trinomial $x^{2}-2 x+2 a$ is $2 a-1$. Since for the considered values of $a$ we have $2 a-1>0$ (which is true for $a>1 / 2$), the maximum value of $f(x)$ is $M=\frac{700}{2 a-1}$. Next, the condition $M>10$ (for $2 a-1>0$) is equivalent to the following conditions: $700>10(2 a-1) \Leftrightarrow$ $71>2 a$. Among the natural numbers $a=1,2, \ldots, 100$, the last inequality is satisfied by the first 35 values.
|
35
|
Algebra
|
olympiads
| null | null |
\(\boxed{35}\)
|
Problem 6.7. The Amur and Bengal tigers started running in a circle at 12:00, each at their own constant speed. By 14:00, the Amur tiger had run 6 more laps than the Bengal tiger. Then the Amur tiger increased its speed by 10 km/h, and by 15:00, it had run a total of 17 more laps than the Bengal tiger. How many meters is the length of the circle?
|
In the first 2 hours, the Amur tiger ran 6 more laps, i.e., in 1 hour, it ran 3 more laps. If it had not increased its speed, in the first 3 hours, it would have run 9 more laps. However, the increase in speed resulted in an additional $17-9=8$ laps in the third hour. Since it increased its speed by 10 km/h, the additional distance would be 10 km/h $\cdot$ 1 h $=10$ km, and the length of one lap would then be $\frac{10}{8}$ km, or 1250 meters.
|
1250
|
Algebra
|
olympiads
| null | null |
\(\boxed{1250}\)
|
7.2 There were 25 sparrows sitting on two bushes. After 5 sparrows flew from the first bush to the second, and 7 sparrows flew away from the second bush, it turned out that there were twice as many sparrows left on the first bush as on the second. How many sparrows were there on each bush initially?
|
2 On the first bush, there were 17 sparrows, and on the second, there were 8.
After 7 sparrows flew away, 18 remained. At this point, there were twice as many sparrows on the first bush as on the second. This means there were 12 sparrows on the first bush and 6 on the second. If we return 7 sparrows to the second bush and then move five sparrows from the second bush to the first, we will return to the initial situation. As a result, we get 12 + 5 = 17 sparrows on the first bush, and 6 + 7 - 5 = 8 sparrows on the second.
|
17
|
Algebra
|
olympiads
| null | null |
\(\boxed{17}\)
|
7.5. Find all three-digit numbers $\mathrm{N}$ such that the sum of the digits of the number $\mathrm{N}$ is 11 times smaller than the number $\mathrm{N}$ itself (do not forget to justify your answer).
|
5. The number 198 is unique.
From the condition, we get the relation $11 \cdot(a+b+c)=100 a+10 b+c$, or $10 c+b=89 a$. In this relation, the left side is a number less than 100. If $a$ is greater than 1, then the right side will be a number greater than 100. Therefore, $a=1$, $c=8$, $b=9$. All-Russian School Olympiad in Mathematics
|
198
|
Number Theory
|
olympiads
| null | null |
\(\boxed{198}\)
|
# 2. Option 1.
Tourists Vitya and Pasha are walking from city A to city B at equal speeds, while tourists Katya and Masha are walking from city B to city A at equal speeds. Vitya met Masha at 12:00, Pasha met Masha at 15:00, and Vitya met Katya at 14:00. How many hours after noon did Pasha meet Katya?
|
The distance between Masha and Katya and their speeds do not change, and the speeds of Vitya and Pasha are equal. Vitya met Katya 2 hours after Masha, so Pasha will also meet Katya 2 hours after Masha, i.e., at 5:00 PM - 5 hours after noon.
|
5
|
Algebra
|
olympiads
| null | null |
\(\boxed{5}\)
|
6. Increase Grisha's catch by $40 \%$ and Vasya's catch by $20 \%$.
Grisha, the most resourceful of them, calculated that their total catch in each case would increase by 5, 10, and 9 kg respectively. What was the total catch of the friends (in kilograms) before meeting with Shapka?
|
Let the harvest of Vasya, Misha, and Grisha be denoted by $x, y, z$ respectively. Then, $0.4 x + 0.2 y = 5 ; 0.4 y + 0.2 z = 10 ; 0.4 z + 0.2 x = 9$. Adding the equations, we get $0.6(x + y + z) = 24$, from which $x + y + z = 40$.
|
40
|
Algebra
|
olympiads
| null | null |
\(\boxed{40}\)
|
# 7. Option 1.
Unit cubes were used to assemble a large parallelepiped with sides greater than 3. Two cubes will be called adjacent if they touch by faces. Thus, one cube can have up to 6 neighbors. It is known that the number of cubes that have exactly 6 neighbors is 429. Find the number of cubes that have exactly 4 neighbors.
|
Let $a, b$ and $c$ be the lengths of the sides of the large parallelepiped. Then, the number of cubes with exactly 6 neighbors is: $(a-2)(b-2)(c-2)$. Since each of the factors $a-2, b-2$, and $c-2$ is greater than 1 and their product equals the product of the three prime numbers 3, 11, and 13, these numbers must be 3, 11, and 13 in some order. The number of cubes with exactly 4 neighbors is $4(a-2+b-2+c-2)$ (since each such cube is adjacent to exactly one edge). Thus, we get the answer: $4(3+11+13)=108$.
|
108
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{108}\)
|
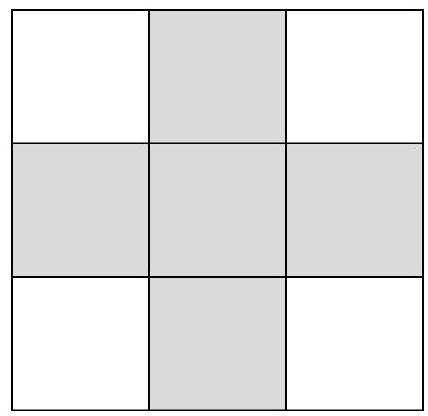
Problem 8.2. The numbers from 1 to 9 were placed in the cells of a $3 \times 3$ table such that the sum of the numbers on one diagonal is 7, and on the other - 21. What is the sum of the numbers in the five shaded cells?
|
Note that 7 can be represented uniquely as the sum of numbers from 1 to 9 - this is $1+2+4=7$.
Let's look at the other diagonal with a sum of 21. The largest possible value of the sum in it is $9+8+4=21$ (since the number in the central cell is no more than 4). Therefore, it must contain the numbers $9,8,4$.
Thus, the number 4 is in the central cell, and the numbers 1, 2, 8, and 9 are at the corners. Now it is not difficult to find the sum of the numbers in the shaded cells: $3+4+5+6+7=25$.
|
25
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{25}\)
|
9.1 The sum of 100 numbers is 1000. The largest of these numbers was doubled, and some other number was decreased by 10. After these actions, the sum of all the numbers did not change. Find the smallest of the original numbers.
|
1 The sum of 100 numbers is 1000. The largest of these numbers was doubled, and some other number was decreased by 10. After these actions, the sum of all the numbers did not change. Find the smallest of the original numbers.
Otvet: 10.
$\boldsymbol{P e s h e n i e : ~ P u s t ь ~} M$ - the largest number, $t$ - some other number. According to the condition $2 M+t-10=M+t$, from which $M=10$. All other numbers are not greater than 10, and if at least one of them is less than 10, then the sum of all 100 numbers will be less than $100 \cdot 10=1000$. Therefore, all the numbers out of these 100 are equal to 10.
|
10
|
Algebra
|
olympiads
| null | null |
\(\boxed{10}\)
|
10.3. Let $n$ - be a natural number. What digit stands immediately after the decimal point in the decimal representation of the number $\sqrt{n^{2}+n}$?
|
We will prove that $(n+0.4)^{2} < 0.8$. The last inequality is true for any natural $n$.
2) $n^{2}+n < (n+0.5)^{2} \Leftrightarrow n < n+0.25$, which is obvious.
Evaluation Criteria.
“+” A complete and justified solution is provided
“Ғ” The correct answer is provided, but only one of the two required inequalities is proven
“-” The correct answer is obtained by considering specific examples
“-” Only the answer is provided
“-” The problem is not solved or is solved incorrectly
|
4
|
Number Theory
|
olympiads
| null | null |
\(\boxed{4}\)
|
11.1. Arkady, Boris, and Vasili decided to run the same distance, consisting of several laps. Arkady ran each lap 2 minutes faster than Boris, and Boris ran 3 minutes faster than Vasili, and all of them ran at a constant speed. When Arkady finished the distance, Boris had one lap left to run, and Vasili had two laps left. How many laps did the distance consist of? Provide all possible answers and explain why there are no others.
|
Let the distance be $n$ laps, and Arkady takes $t$ minutes per lap. Then in $n t$ minutes, Arkady runs the entire distance. In this time, Boris runs one lap less, and Vasily runs two laps less. Therefore, $n t=(n-1)(t+2)$ and $n t=(n-2)(t+5)$. From this, it follows that $2 n=t+2$ and $5 n=2 t+10$, so $n=5 n-4 n=(2 t+10)-2 \cdot(t+2)=6$. Note that in this case, $t=10$, and all conditions are satisfied.
Comment: Only the answer - 2 points.
Remark: From the text of the problem, it follows that the problem has at least one solution. Therefore, if it is proven that there can be no other solutions besides $n=6$, it is not necessary to check this solution.
|
6
|
Algebra
|
olympiads
| null | null |
\(\boxed{6}\)
|
Problem 8.2. The numbers from 1 to 9 were placed in the cells of a $3 \times 3$ table such that the sum of the numbers on one diagonal is 7, and on the other - 21. What is the sum of the numbers in the five shaded cells?
|
Note that 7 can be represented uniquely as the sum of numbers from 1 to 9 - this is $1+2+4=7$.
Let's look at the other diagonal with a sum of 21. The largest possible value of the sum in it is $9+8+4=21$ (since the number in the central cell is no more than 4). Therefore, it must contain the numbers $9,8,4$.
Thus, the number 4 is in the central cell, and the numbers 1, 2, 8, and 9 are at the corners. Now it is not difficult to find the sum of the numbers in the shaded cells: $3+4+5+6+7=25$.
|
25
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{25}\)
|
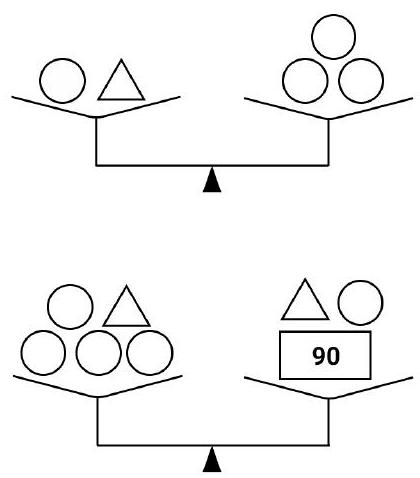
Problem 6.1. The set includes 8 weights: 5 identical round, 2 identical triangular, and one rectangular weight weighing 90 grams.
It is known that 1 round and 1 triangular weight balance 3 round weights. Additionally, 4 round weights and 1 triangular weight balance 1 triangular, 1 round, and 1 rectangular weight.
How much does the triangular weight weigh?
|
From the first weighing, it follows that 1 triangular weight balances 2 round weights.
From the second weighing, it follows that 3 round weights balance 1 rectangular weight, which weighs 90 grams. Therefore, a round weight weighs $90: 3=30$ grams, and a triangular weight weighs $30 \cdot 2=60$ grams.
|
60
|
Algebra
|
olympiads
| null | null |
\(\boxed{60}\)
|
3. The numbers $1,2,3,4,5,6,7,8,9$ are written into the cells of a $3 \times 3$ table. After that, all possible sums of numbers standing in adjacent (by side) cells are written down in a notebook. What is the smallest number of different numbers that could have been written in the notebook?
|
# Solution:
Consider the number in the central cell of the table. Next to it are 4 different neighbors - they give 4 different sums with the central number, so there are already at least 4 different sums written down. An example where there are exactly 4 of them exists (one is shown on the right, the sums are $8,9,10,11$).
## Criteria:
There is an example with 4 different sums (to be checked!) - 2 points.
There is an estimate - that is, an explanation of why it is impossible to have fewer than 4 different sums - 3 points. Both a correct estimate and a correct example - 7 points.
|
4
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{4}\)
|
1. Option 1. To a confectionery factory for cake packaging, 5 rolls of ribbon, each 60 m long, were delivered. How many cuts need to be made to get pieces of ribbon, each 1 m 50 cm long?
|
From one roll, 40 pieces of ribbon, each 1 m 50 cm long, can be obtained. For this, 39 cuts are needed. Therefore, a total of $5 \cdot 39=195$ cuts are required.
|
195
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{195}\)
|
# 5. Option 1.
An apple, three pears, and two bananas together weigh 920 g; two apples, four bananas, and five pears together weigh 1 kg 710 g. How many grams does a pear weigh?
|
From the first condition, it follows that two apples, four bananas, and six pears together weigh 1 kg 840 g. Therefore, a pear weighs $1840-1710=130$ g.
|
130
|
Algebra
|
olympiads
| null | null |
\(\boxed{130}\)
|
10.6. On the board, three natural numbers were written: two ten-digit numbers $a$ and $b$, as well as their sum $a+b$. What is the maximum number of odd digits that could have been written on the board?
(I. Bogdanov, P. Kozhevnikov)
|
Note that the number $a+b$ has no more than 11 digits, so in total, no more than 31 digits are written on the board. At the same time, all three numbers $a, b, a+b$ cannot be odd simultaneously. Therefore, one of their last three digits is even, which means that there are no more than 30 odd digits written.
Let's provide an example showing that there could be exactly 30 odd digits:
$5555555555+5555555555=11111111110$.
Remark. There are many examples with 30 odd digits, for instance, $3999999999+7999999999=11999999998$.
Comment. Only the answer without any correct explanation - 0 points. Only the proof that there are no more than $30-3$ points. Only a correct example with 30 odd digits - 4 points.
|
30
|
Number Theory
|
olympiads
| null | null |
\(\boxed{30}\)
|
Problem 6.4. Misha made himself a homemade dartboard during the summer at the cottage. The round board is divided by circles into several sectors - darts can be thrown into it. Points are awarded for hitting a sector as indicated on the board.
Misha threw 8 darts 3 times. The second time he scored twice as many points as the first time, and the third time he scored 1.5 times as many points as the second time. How many points did he score the second time?
|
The smallest possible score that can be achieved with eight darts is $3 \cdot 8=24$. Then, the second time, Misha scored no less than $24 \cdot 2=48$ points, and the third time, no less than $48 \cdot 1.5=72$.
On the other hand, $72=9 \cdot 8$ is the highest possible score that can be achieved with eight darts. Therefore, the third time, Misha scored exactly 72 points, and the second time, exactly 48.
|
48
|
Algebra
|
olympiads
| null | null |
\(\boxed{48}\)
|
Problem 8.2. In the chat of students from one of the schools, a vote was held: "On which day to hold the disco: October 22 or October 29?"
The graph shows how the votes were distributed an hour after the start of the voting.
Then, 80 more people participated in the voting, voting only for October 22. After that, the voting ended. The final distribution of votes is also shown on the graph.
How many people participated in the voting?
|
Let $x$ be the number of people who voted an hour after the start. From the left chart, it is clear that $0.35 x$ people voted for October 22, and $-0.65 x$ people voted for October 29.
In total, $x+80$ people voted, of which $45\%$ voted for October 29. Since there are still $0.65 x$ of them, we get the equation
$0.65 x=0.45(x+80)$, from which we find $x=180$. Therefore, a total of $180+80=260$ people participated in the voting.
|
260
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{260}\)
|
1. Seven friends entered a cafe and ordered 3 small cups of coffee, 8 medium cups, and 10 large cups. The volume of a small cup is half the volume of a medium cup, and the volume of a large cup is three times the volume of a small cup. How should the friends divide the cups of coffee among themselves so that everyone drinks an equal amount of coffee? Pouring coffee from one cup to another is not allowed.
|
Let's call the amount of coffee in a small cup a "norm". Then, in total, we have $3+8 \times 2+10 \times 3=49$ norms. Since there are seven friends, each should get 7 norms.
We divide as follows: 1 small + 2 large - 3 people; 2 medium + 1 large - 4 people.
Criteria. A correct example - 7 points. No additional reasoning is required. If the result is obtained that each person needs 7 "norms", but the example is not shown (or the example is incorrect) - $\mathbf{1}$ point.
Incorrect example, lack of example - 0 points.
|
1
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{1}\)
|
2. Vasya claims that the number of his friends who are good at mathematics is not less than $96.8\%$ and not more than $97.6\%$. It is known that the number of Vasya's friends does not exceed 150. Determine the largest number within the specified range that cannot be the number of Vasya's friends.
|
# Solution
Let $\mathrm{N}$ be the number of Vasya's friends. The number $x$ of Vasya's friends who are not good at math is in the range $0.024 N < x < 0.032 N$, then for $x=1, 31 \frac{1}{4} < N < 41 \frac{2}{3}$; for $x=2, 62 \frac{1}{3} < N < 83 \frac{1}{3}$; for $x=3, 93 \frac{3}{4} < N < 125$; for $x=4, 125 < N < 166 \frac{2}{3}$. Thus, the largest sought number is 125.
## Grading Criteria
Correct answer with justification - 7 points.
In case of an arithmetic error - no more than 4 points.
#
|
125
|
Number Theory
|
olympiads
| null | null |
\(\boxed{125}\)
|
1. Petya was exchanging stickers. He trades one sticker for 5 others. At first, he had 1 sticker. How many stickers will he have after 30 exchanges?
|
After each exchange, the number of Petya's stickers increases by 4 (one sticker disappears and 5 new ones appear). After 30 exchanges, the number of stickers will increase by $30 * 4 = 120$. Initially, Petya had one sticker, so after 30 exchanges, he will have $1 + 120 = 121$.
|
121
|
Number Theory
|
olympiads
| null | null |
\(\boxed{121}\)
|
1. In the game "Sportlotto-Shish," the main prize is drawn according to the following rules. Each person in the studio independently writes down any number of different pairs of different integers from the set from 1 to 5. If some participants have written down the same pairs, these participants share the main prize. How many participants should be in the studio to ensure that the prize is definitely awarded?
|
A total of different pairs can be formed $5 * 4 / 2=10$. It is taken into account that the digits in the pair are different and the order of the digits within the pair does not matter. Each pair can be written down or not written down by the participant. A total of different sets can be formed $2^{10}=1024$. Among them, there is an empty set (no pair is written down). In total, 1023 sets. For someone to have matching sets, the presence of 1024 people is necessary.
Comment. It is essential to exclude the empty set and then add one person (by the pigeonhole principle). A correct answer without excluding the empty set is rated 1 point.
|
1024
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{1024}\)
|
2. In a row, 33 weights are arranged in ascending order. It is known that any four consecutive weights can be distributed on two scales so that equilibrium is achieved. The third weight weighs 9 g, and the ninth weighs 33 g. How much does the 33rd weight weigh?
|
Let the weights of the weights be $a_{1}<a_{2}<\cdots<a_{33}$. For all $k=1,2, \ldots, 30$ the equalities $a_{k}+a_{k+3}=a_{k+1}+a_{k+2}$, equivalent to $a_{k+3}-a_{k+2}=$ $a_{k+1}-a_{k}$, hold. Let $a_{4}-a_{3}=a_{2}-a_{1}=d$ and $a_{5}-a_{6}=a_{3}-a_{2}=\mathrm{c}$, then $a_{6}-$ $a_{5}=a_{4}-a_{3}=d, a_{7}-a_{6}=a_{5}-a_{4}=$ c and so on. From this, $a_{1}+d+c=$ $a_{3}=9$ and $a_{1}+4 d+4 c=a_{9}=33$. From the difference of the last equalities we get $d+c=8$, and then $a_{1}=1$. We calculate $a_{33}=a_{1}+16(d+c)=129$.
Comment. An incomplete solution, brought to a system of two equations connecting $a_{1}, d, c,-4$ points.
|
129
|
Number Theory
|
olympiads
| null | null |
\(\boxed{129}\)
|
Problem 2. On the board, there are 2017 digits. From these, several numbers were formed, the sums of the digits of these numbers were calculated, and then the sum of all the numbers was subtracted by the sum of the sums of their digits. The resulting number was broken down into digits, and the above operation was repeated again. After performing this operation several times, only one digit remained on the board for the first time. What is this digit?
|
Since the difference between a number and the sum of its digits is divisible by 9, the first operation will result in a number that is a multiple of 9. Moreover, if we take the sum of several numbers and subtract the sum of the digits of these numbers, the result will also be a multiple of 9. Continuing the calculations, we will get numbers that are multiples of 9 but decreasing in absolute value. In the end, the first single-digit number we obtain must be divisible by 9, and that is only 9.
|
9
|
Number Theory
|
olympiads
| null | null |
\(\boxed{9}\)
|
7.5. The numbers from 1 to 20 are arranged in a circle. We will paint a number blue if it is divisible without a remainder by the number to its left. Otherwise, we will paint it red. What is the maximum number of blue numbers that could be in the circle?
|
# Solution.
Evaluation. It is obvious that numbers cannot be blue if the number to their left is greater than or equal to 11. That is, no more than 10 numbers can be blue.
Example. As an example, both any correct arrangement and a correct algorithm are counted. An example of a correct algorithm.
1) write down the number 20
2) if the last written number $=2 \mathrm{k}$, then write the number $\mathrm{k}$ to its left, otherwise write the largest unused number to its left.
3) while there are unused numbers - repeat step 2.
## Criteria.
7 points for having both the evaluation and a correct example
4 points for only the example
3 points for only the evaluation.
|
10
|
Number Theory
|
olympiads
| null | null |
\(\boxed{10}\)
|
# 3.1. Condition:
The number 4597 is displayed on the computer screen. In one move, it is allowed to swap any two adjacent digits, but after this, 100 is subtracted from the resulting number. What is the largest number that can be obtained by making no more than two moves?
|
## Solution.
The first digit cannot exceed 8, since to obtain the other digits, you need to move the nine forward by two places and subtract one from it. Note that in any other example, the first digit will be less than 8, as we can only get an eight from a nine, and all other digits are less than 9. The only way to get the digit 8 in the first position is to move the 9 forward twice.
#
|
8357
|
Number Theory
|
olympiads
| null | null |
\(\boxed{8357}\)
|
3.3. A package of milk with a volume of 1 liter cost 80 rubles. Recently, in order to save money, the manufacturer reduced the volume of the package to 0.9 liters, and increased the price to 99 rubles. By what percentage did the manufacturer's revenue increase?
|
We will calculate by what percentage the cost of 9 liters of milk has increased. Before the increase, 9 liters cost $9 \cdot 80=720$ rubles, and after the increase - $99 \cdot 10=990$ rubles. The increase amounts to 270 rubles for 9 liters. This amount previously cost 720 rubles. This is $\frac{270}{720} \cdot 100 \% = 37.5 \%$
|
37.5
|
Algebra
|
olympiads
| null | null |
\(\boxed{37.5}\)
|
4.1. Galia thought of a number, multiplied it by N, then added N to the result, divided the resulting number by N, and subtracted N. In the end, she got a number that is 2021 less than the originally thought number. What is N?
|
Let the number she thought of be $\mathrm{k}$, then after two operations, she will have the number $\mathrm{kN}+\mathrm{N}$, and after division, she will have the number $\mathrm{k}+1$, which is 1 more than the number she thought of. And when she subtracts $\mathrm{N}$, the result will be a number that is $\mathrm{N}-1$ less than the original number.
|
2022
|
Algebra
|
olympiads
| null | null |
\(\boxed{2022}\)
|
4.2. Galia thought of a number, multiplied it by $\mathrm{N}$, then added $\mathrm{N}$ to the result, divided the resulting number by N, and subtracted N. In the end, she got a number that is 7729 less than the originally thought number. What is N?
|
Let the number she thought of be $\mathrm{k}$, then after two operations, she will have the number $\mathrm{kN}+\mathrm{N}$, and after division, she will have the number $\mathrm{k}+1$, which is 1 more than the number she thought of. And when she subtracts $\mathrm{N}$, the result will be a number that is $\mathrm{N}-1$ less than the initial number.
|
7730
|
Algebra
|
olympiads
| null | null |
\(\boxed{7730}\)
|
4.3. Galia thought of a number, multiplied it by N, then added N to the result, divided the resulting number by N, and subtracted N. In the end, she got a number that is 100 less than the originally thought number. What is N?
|
Let the number she thought of be $\mathrm{k}$, then after two operations, she will have the number $\mathrm{kN}+\mathrm{N}$, and after division, she will have the number $\mathrm{k}+1$, which is 1 more than the number she thought of. And when she subtracts $\mathrm{N}$, the result will be a number that is $\mathrm{N}-1$ less than the original number.
|
101
|
Algebra
|
olympiads
| null | null |
\(\boxed{101}\)
|
5.4. For the celebration of the Name Day in the 5th grade parallel, several pizzas were ordered. 10 pizzas were ordered for all the boys, with each boy getting an equal share. Each girl also received an equal share, but half as much as each boy. How many pizzas were ordered if it is known that there are 17 girls in this parallel, and there are more boys than girls? Pizzas can be divided into parts.
|
Let the number of boys be $m$, and the number of pizzas that the girls got be $x$. If each boy had eaten as much as each girl, the boys would have eaten 5 pizzas. Then $m: 17 = 5: x$, from which $m x = 85$. The number 85 has only one divisor greater than 17, which is 85. Therefore, $m=85, x=1$, the answer is $10+1=11$ pizzas.
|
11
|
Algebra
|
olympiads
| null | null |
\(\boxed{11}\)
|
8.2. In a cinema, five friends took seats numbered 1 to 5 (the leftmost seat is number 1). During the movie, Anya left to get popcorn. When she returned, she found that Varya had moved three seats to the right, Galia had moved one seat to the left, and Diana and Elia had swapped places, leaving the edge seat for Anya. Which seat did Anya occupy before she stood up?
|
Let's see how the seat number changed for everyone except Anya. Varya's seat number increased by 3, Galia's decreased by 1, and the sum of Diana's and Eli's seat numbers did not change. At the same time, the total sum of the seat numbers did not change, so Anya's seat number must have decreased by 2. But then the seat left for her cannot be seat 5 (since there is no seat 6), so the seat left for her must be seat 1, and initially, she had seat 3.
|
3
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{3}\)
|
3. Misha calculated the products $1 \times 2, 2 \times 3$, $3 \times 4, \ldots, 2017 \times 2018$. For how many of them is the last digit zero?
|
The last digit of the product depends on the last digits of the factors. In the sequence of natural numbers, the last digits repeat every ten. In each ten, in the sequence of products, four products end in zero: ... $4 \times \ldots 5, \ldots 5 \times \ldots 6, \ldots 9 \times \ldots 0, \ldots 0 \times \ldots 1$. ... There are 201 complete tens. And at the end, there are seven more products, two of which end in zero.
Thus, a total of $4 \times 201 + 2 = 806$ products end in zero.
Criteria. Any correct solution: 7 points.
In the solution, two zeros from the last incomplete ten are lost: 4 points.
Only the correct answer is provided: 1 point.
|
806
|
Number Theory
|
olympiads
| null | null |
\(\boxed{806}\)
|
Problem 3. During a math test, Oleg was supposed to divide a given number by 2, and then add 6 to the result. But he hurried and instead multiplied the given number by 2, and then subtracted 6 from the result. Nevertheless, he got the correct answer. What number was given to Oleg
|
Since Oleg multiplied the number by 2 instead of dividing it, he got a result that is four times greater than the required one. This means that the difference between these two results is three times greater than the required result. However, according to the condition, this difference is equal to $6+6=12$. Therefore, the required result is $12: 3=4$. Then the guessed number is $4 \cdot 2=8$.
|
8
|
Algebra
|
olympiads
| null | null |
\(\boxed{8}\)
|
Problem 5. A messenger was riding a horse to deliver a message to Ilya Muromets. At some point, he noticed that Ilya Muromets had passed by him (and continued walking in the opposite direction). After 10 seconds (when the horse stopped), the messenger dismounted and ran to catch up with Ilya. How many seconds will it take for the messenger to deliver the message if he runs twice as fast as Ilya Muromets, but five times slower than the galloping horse?
|
Let Ilya Muromets walk at a speed of $x$ meters per second. Then the messenger's speed is $2x$, and the horse's speed is $10x$. Therefore, 10 seconds after the meeting, the distance between the messenger and the horse will be $10 \cdot x$ (Ilya Muromets has walked) $+10 \cdot 10 x$ (the horse has traveled to a complete stop) $=110 x$. After this, the closing speed of the messenger and Ilya Muromets is $2x-x=x$. Thus, the messenger will deliver the message in 110 seconds.
|
110
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{110}\)
|
Problem 2. A family of four octopuses came to a shoe store (each octopus has 8 legs). The father octopus already had half of his legs booted, the mother octopus had only 3 legs booted, and their two sons had 6 legs booted each. How many boots did they buy if they left the store fully booted?
|
The daddy octopus had half of his legs booted, that is, 4 legs. Thus, 4 legs were not booted.
The mommy octopus had 3 legs booted, meaning 5 legs were not booted.
Each of the two sons had 6 legs booted, meaning 2 legs were not booted.
Thus, a total of $4+5+2+2=13$ boots were bought.
## Criteria
## 3 p. Only the correct answer is provided.
4 6. The correct answer is provided, along with the calculations used to obtain it.
|
13
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{13}\)
|
1. Variant 1.
Masha is distributing tennis balls into identical boxes. If she uses 4 boxes, there is still room for 8 more balls in the last box, and if she uses 3 boxes, 4 balls will not fit into the boxes. How many balls is one box designed to hold?
|
Method 1
Notice that if the balls are in 3 boxes, there are 4 tennis balls left. Take these 4 balls and put them in the fourth box. According to the condition, there will still be room for 8 more balls in this box. This means that the box can hold a total of 12 balls.
Method 2.
Let the box hold $x$ balls. Then $3 x+4=4 x-8$. From this, $x=12$.
|
12
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{12}\)
|
3. Variant 1.
A natural number is written on the board. Five schoolchildren said the following about it:
- Pete: “This number is greater than $10$.”
- Kolya: “This number is not less than $11$.”
- Vasya: “This number is greater than $12$.”
- Dima: “This number is less than $12$.”
- Oleg: “This number is not greater than $12$.”
Find the maximum possible number of correct statements.
|
All five answers could not have been correct, since Vasya's and Dima's answers contradict each other. Four answers could have been correct if the number 11 was written on the board.
|
4
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{4}\)
|
4. Variant 1.
In the number, two digits were swapped, and as a result, it increased by more than 3 times. The resulting number is 8453719. Find the original number.
|
When the number 8453719 is reduced by at least 3 times, the result is a number less than 3000000. Therefore, 8 was swapped with a digit less than 3, and the only such digit is 1.
|
1453789
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{1453789}\)
|
7. Variant 1.
Petya wrote 9 consecutive natural numbers on the board. Kolya calculated their sum and got the answer 43040102. It turned out that he made a mistake only in the first digit of the sum. What should the first digit be
|
Let the consecutive natural numbers be $a-4, a-3, \cdots, a+3, a+4$. The sum of nine consecutive numbers is divisible by 9, indeed, this sum is equal to $(a-4)+(a-3)+\cdots+(a+3)+(a+4)=9a$. Therefore, the desired sum must be divisible by 9. This means that the sum of the digits of the obtained answer must also be divisible by 9. The sum of all digits except the first one is 10. Therefore, the first digit must be 8. A suitable number would be 83040102.
|
8
|
Number Theory
|
olympiads
| null | null |
\(\boxed{8}\)
|
# 8. Variant 1.
101 natural numbers are written in a circle. It is known that among any 5 consecutive numbers, there will be at least two even numbers. What is the minimum number of even numbers that can be among the written numbers?
|
Consider any 5 consecutive numbers. Among them, there is an even number. Fix it, and divide the remaining 100 into 20 sets of 5 consecutive numbers. In each such set, there are at least two even numbers. Thus, the total number of even numbers is no less than $1+2 \cdot 20=41$. Such a situation is possible. Number the numbers in a circle. The even numbers can be those with numbers $1,3,6$, $8,11, \ldots, 98,101$ (the number with number 1 is even, and in each set of 5 numbers with numbers $5 \mathrm{k}+2$, $5 \mathrm{k}+3,5 \mathrm{k}+4,5 \mathrm{k}+5,5 \mathrm{k}+6$, the numbers with numbers $5 \mathrm{k}+3$ and $5 \mathrm{k}+6$ are even).
|
41
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{41}\)
|
10.4. Let x be some natural number. Among the statements:
$2 \times$ greater than 70
x less than 100
$3 x$ greater than 25
x not less than 10
x greater than 5
three are true and two are false. What is x
|
The first statement is equivalent to x > 35, and the third statement is equivalent to $\mathrm{x}>8$, since x is a natural number. The first statement is false, because if it were true, then the third, fourth, and fifth statements would also be true, i.e., there would be at least 4 true statements. Therefore, x does not exceed 35. From this, it follows that the second statement is true. But then the fourth statement is false (otherwise, the third and fifth statements would also be true, and again we would have at least 4 true statements). Therefore, statements 3 and 5 are true. And from the falsity of the fourth statement and the truth of the third statement, it immediately follows that $x=9$.
|
9
|
Inequalities
|
olympiads
| null | null |
\(\boxed{9}\)
|
1. (7 points) In a three-digit number, the first digit (hundreds place) was increased by 3, the second digit by 2, and the third digit by 1. As a result, the number increased by 4 times. Provide an example of such an original number.
Answer: 107.
|
The answer can be found in the following way. Let $x$ be the desired number. Then the condition of the problem immediately leads to the equation $x+321=4x$, the only solution of which is $x=107$.
Criteria. Correct answer, even without any comments: 7 points.
Incorrect answer: 0 points.
|
107
|
Number Theory
|
olympiads
| null | null |
\(\boxed{107}\)
|
2. (7 points) A movie ticket cost 300 rubles. When the price was reduced, the number of visitors increased by 50 percent, and the cinema's revenue increased by 35 percent. How many rubles does one ticket cost now?
|
Let the price of the new ticket be $s$ rubles. Suppose the initial number of visitors was $N$, and after increasing by $50 \%$ it became $1.5 N$. Then, according to the condition, the current revenue of the cinema $1.5 N \cdot s$ is $35 \%$ more than $N \cdot 300$, from which we have $1.5 N s = 1.35 \cdot N \cdot 300$, and $s=270$.
Criteria. Any correct solution: 7 points.
Only the correct answer is provided: 1 point.
|
270
|
Algebra
|
olympiads
| null | null |
\(\boxed{270}\)
|
3. (7 points) Given an arithmetic progression. The sum of its first 10 terms is 60, and the sum of its first 20 terms is 320. What can the 15th term of this progression be?
|
Let the first term of the sequence be $a$, and the common difference be $b$. Then the sum of the first 10 terms is $a+(a+b)+\ldots+(a+9b)=$ $10a+45b$. The sum of the first 20 terms is $a+(a+b)+\ldots+(a+19b)=$ $20a+190b$. According to the problem, $10a+45b=60, 20a+190b=320$. Solving the system, we find $a=-3, b=2$. Then the 15th term is $a+14b=25$.
Criteria. Any correct solution: 7 points.
A generally correct solution containing arithmetic errors that do not affect the solution process: 5 points.
Only the answer: 1 point.
|
25
|
Algebra
|
olympiads
| null | null |
\(\boxed{25}\)
|
Problem 6.1. Find any solution to the puzzle
$$
\overline{A B}+A \cdot \overline{C C C}=247
$$
where $A, B, C$ are three different non-zero digits; the notation $\overline{A B}$ represents a two-digit number composed of the digits $A$ and $B$; the notation $\overline{C C C}$ represents a three-digit number consisting only of the digit $C$. Write the three-digit number $\overline{A B C}$ as your answer.
|
The number $\overline{C C C}$ is divisible by 111 and is less than 247, so $A \cdot \overline{C C C}$ is either 111 or 222. In the first case, we get that $\overline{A B}=247-111=136$, which is impossible. In the second case, $\overline{A B}=247-222=25$, that is, $A=2, B=5$, and therefore, $C=1$.
|
251
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{251}\)
|
Problem 6.2. At a ball, princesses and knights gathered - a total of 22 people. The first princess danced with seven knights, the second with eight knights, the third with nine knights, ..., the last danced with all the knights present. How many princesses were at the ball?
|
Note that the number of knights the princess danced with is 6 more than her number. Let there be $x$ princesses in total, then the last one has the number $x$ and danced with all the knights, and there are $x+6$ of them in total. We get that there were $x+$ $(x+6)=2x+6=22$ people at the ball, which means there were 8 princesses.
|
8
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{8}\)
|
Problem 6.3. Dima, Misha, and Yura decided to find out who among them is the most athletic. For this, they held 10 competitions. The winner received 3 points, the second place 1 point, and the third place received nothing (in each competition, there was a first, second, and third place). In total, Dima scored 22 points, and Misha scored 8 points. How many points did Yura score?
|
In each competition, the boys in total received $3+1+0=4$ points. For all competitions, they scored $4 \cdot 10=40$ points. Dima and Misha in total scored $22+8=30$ points, so the remaining $40-30=10$ points were scored by Yura.
|
10
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{10}\)
|
Problem 6.4. On her birthday, Katya treated her classmates with candies. After giving out some candies, she noticed that she had 10 more candies left than Artem received. After that, she gave everyone one more candy, and it turned out that all the children in the class (including Katya) had the same number of candies. How many classmates does Katya have?
|
Initially, the number of candies Kati and Artyom had differed by 10. When Kati gave everyone one more candy, the number of candies Artyom had increased by 1, and the number of candies Kati had decreased by the number of her classmates, and they ended up with the same amount. This means that 10 is the number of her classmates plus 1. Therefore, Kati has 9 classmates.
|
9
|
Algebra
|
olympiads
| null | null |
\(\boxed{9}\)
|
Problem 9.1. In a store, there are 20 items, the costs of which are different natural numbers from 1 to 20 rubles. The store has decided to have a promotion: when buying any 5 items, one of them is given as a gift, and the customer chooses which item to receive for free. Vlad wants to buy all 20 items in this store, paying as little as possible. How many rubles will he need? (Each of the 20 items is sold in 1 copy.)
|
Vlad can take advantage of the offer no more than 4 times, so he will get no more than 4 items for free. The total cost of these 4 items does not exceed $17+18+$ $19+20$ rubles. Therefore, the rubles Vlad needs are not less than
$$
(1+2+3+\ldots+20)-(17+18+19+20)=1+2+3+\ldots+16=\frac{16 \cdot 17}{2}=136
$$
We will show that 136 rubles will definitely be enough for him. He can make purchases of items with the following costs: $(1,2,3,4,17),(5,6,7,8,18),(9,10,11,12,19),(13,14,15,16,20)$. If Vlad takes the last item for free in each purchase, he will spend exactly 136 rubles.
|
136
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{136}\)
|
Problem 9.2. Vanya thought of two natural numbers, the product of which equals 7200. What is the greatest value that the GCD of these numbers can take?
|
Since each of these numbers is divisible by their GCD, their product is divisible by the square of this GCD. The greatest exact square that divides the number $7200=2^{5} \cdot 3^{2} \cdot 5^{2}$ is $3600=\left(2^{2} \cdot 3 \cdot 5\right)^{2}$, so the GCD of the two numbers in question does not exceed 60. The GCD can be equal to 60 if the two numbers in question are 60 and 120.
|
60
|
Number Theory
|
olympiads
| null | null |
\(\boxed{60}\)
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.