problem
stringlengths 17
4.31k
| solution_hint
stringlengths 49
6.77k
| answer
stringlengths 1
44
⌀ | problem_type
stringclasses 8
values | source
stringclasses 2
values | level
stringclasses 3
values | type
stringclasses 7
values | solution
stringlengths 13
56
|
|---|---|---|---|---|---|---|---|
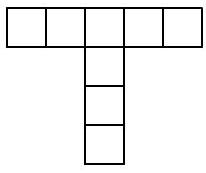
Problem 4.3. How many rectangles exist on this picture with sides running along the grid lines? (A square is also a rectangle.)
|
In a horizontal strip $1 \times 5$, there are 1 five-cell, 2 four-cell, 3 three-cell, 4 two-cell, and 5 one-cell rectangles. In total, $1+2+3+4+5=15$ rectangles.
In a vertical strip $1 \times 4$, there are 1 four-cell, 2 three-cell, 3 two-cell, and 4 one-cell rectangles. In total, $1+2+3+4=10$ rectangles. At the same time, one one-cell rectangle at the intersection of the strips is counted twice (and only it is). Therefore, the answer to the problem is the number $15+10-1=24$.
|
24
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{24}\)
|
.5. Write the largest eight-digit number in which all even digits are present. (Even digits: $0,2,4,6,8$.)
|
The number 99986420 meets the condition of the problem. Suppose there exists a larger eight-digit number. It is clear that its first three digits must be nines. Since there are only 5 even digits, the last five digits are $0,2,4,6,8$ in some order. But then such an eight-digit number cannot exceed 99986420, a contradiction.
|
99986420
|
Number Theory
|
olympiads
| null | null |
\(\boxed{99986420}\)
|
Problem 4.8. If in the number 79777 the digit 9 is crossed out, the number 7777 is obtained. How many different five-digit numbers exist from which 7777 can be obtained by crossing out one digit?
|
Note that 77777 is one of such numbers. Next, we will consider five-digit numbers where to get 7777, we need to strike out a digit that is not 7.
If the first digit in the number is struck out, there are 8 options for it: $1,2,3,4,5,6,8,9$. If, however, the second, third, fourth, or fifth digit in the number is struck out, there are 9 options for it: $0,1,2,3,4,5,6,8,9$.
Obviously, all the corresponding numbers are distinct, and there are $1+8+9+9+9+9=45$ of them.
## 5th grade
|
45
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{45}\)
|
Problem 5.1. Sasha wrote down on the board all two-digit numbers divisible by 6, and then erased those that do not end in 4. What is the largest number that ended up on the board?
|
Let's take the largest two-digit number divisible by 6, which is 96, and sequentially subtract 6 from it. This way, we will go through all numbers divisible by 6 in descending order. We will stop at the first one that ends in 4, which is what we need.
$$
96 \rightarrow 90 \rightarrow 84
$$
|
84
|
Number Theory
|
olympiads
| null | null |
\(\boxed{84}\)
|
Problem 5.3. A cuckoo clock is hanging on the wall. When a new hour begins, the cuckoo says "cuckoo" a number of times equal to the number the hour hand points to (for example, at 19:00, "cuckoo" sounds 7 times). One morning, Maxim approached the clock when it was 9:05. He started turning the minute hand until he advanced the clock by 7 hours. How many times did "cuckoo" sound during this time?

|
The cuckoo will say "cuckoo" from 9:05 to 16:05. At 10:00 it will say "cuckoo" 10 times, at 11:00 - 11 times, at 12:00 - 12 times. At 13:00 (when the hand points to the number 1) "cuckoo" will sound 1 time. Similarly, at 14:00 - 2 times, at 15:00 - 3 times, at 16:00 - 4 times. In total
$$
10+11+12+1+2+3+4=43
$$
|
43
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{43}\)
|
Problem 5.4. At the end-of-the-year school dance, there were twice as many boys as girls. Masha counted that there were 8 fewer girls, besides herself, than boys. How many boys came to the dance?
|
Let there be $d$ girls at the disco, then there are twice as many boys, i.e., $d+d$. The number of girls, excluding Masha, is $d-1$ (all except herself).
Since there are 8 more boys than the other girls, excluding Masha, then $d+d=(d-1)+8$. From this, it follows that $d=7$, so the total number of boys is $7+7=14$.
|
14
|
Algebra
|
olympiads
| null | null |
\(\boxed{14}\)
|
Problem 6.2. For preparing one portion of salad, 2 cucumbers, 2 tomatoes, 75 grams of feta cheese, and 1 pepper are required. The restaurant's warehouse has 60 peppers, 4.2 kg of feta cheese, 116 tomatoes, and 117 cucumbers. How many portions can be made?
|
The pepper will last for $60: 1=60$ servings.
The feta cheese will last for $4200: 75=56$ servings (kilograms converted to grams).
The tomatoes will last for $116: 2=58$ servings.
The cucumbers will last for $117: 2=58.5$, i.e., 58 whole servings.
Since all ingredients must be included in each serving, exactly 56 servings can be prepared.
|
56
|
Other
|
olympiads
| null | null |
\(\boxed{56}\)
|
Problem 6.6. Several oranges (not necessarily of equal weight) were picked from a tree. When they were weighed, it turned out that the weight of any three oranges taken together is less than $5 \%$ of the total weight of the remaining oranges. What is the smallest number of oranges that could have been picked?
|
oranges could have been, for example, if all of them had the same mass $m$, since $\frac{3 m}{61 m}<0.05$.
Suppose there were no more than 63 oranges. Consider the three heaviest oranges with a total mass of $M$. All the other oranges (no more than 60) can be divided into no more than 20 groups, each containing no more than 3 oranges. Obviously, the total mass in each group does not exceed $M$, so the total mass in all groups does not exceed $20 M$. Since $\frac{M}{20 M}=0.05$, the three heaviest oranges account for no less than $5\%$ of the total mass of the other oranges. Contradiction.
|
64
|
Inequalities
|
olympiads
| null | null |
\(\boxed{64}\)
|
Problem 6.7. Petya thinks of a four-digit number of the form $\overline{20 * *}$.
Vasya sequentially checks if the number Petya thought of is divisible by 1, 3, 5, 7, 9, 11, and if it is, Vasya pays Petya 1, 3, 5, 7, 9, or 11 rubles respectively. For example, for the number 2000, Vasya would have paid Petya $1+5=6$ rubles.
What is the maximum number of rubles Petya can receive?
|
Suppose Petya's number is divisible by 9 and by 11. Then it is also divisible by 99. There is exactly one such number in the given range - it is $2079=3^{3} \cdot 7 \cdot 11$. For this number, Petya would receive $1+3+7+9+11=31$ rubles.
If Petya's number is not divisible by 9 or not divisible by 11, then he would receive no more than $1+3+$ $5+7+11=27$ rubles, which is less than 31.
|
31
|
Number Theory
|
olympiads
| null | null |
\(\boxed{31}\)
|
Problem 7.2. Three pirates were dividing a treasure. The first one got a third of the initial number of coins and one more coin, the second one got a quarter of the initial number of coins and five more coins, the third one got a fifth of the initial number of coins and twenty more coins (thus all the coins were distributed). How many coins were in the treasure?
|
Let $m$ be the initial total number of coins in the treasure. The pirates collectively took $\left(\frac{m}{3}+1\right)+\left(\frac{m}{4}+5\right)+\left(\frac{m}{5}+20\right)$ coins. Since they divided the entire treasure, this sum equals $m$. Expanding the brackets in the equation
$$
\left(\frac{m}{3}+1\right)+\left(\frac{m}{4}+5\right)+\left(\frac{m}{5}+20\right)=m
$$
and bringing the fractions to a common denominator, we get $\frac{47}{60} m+26=m$, from which $\frac{13}{60} m=26$, that is, $m=120$.
|
120
|
Algebra
|
olympiads
| null | null |
\(\boxed{120}\)
|
Problem 7.5. If a platoon of soldiers is divided into brigades of 7 people, then 2 people will not fit into any brigade. If the platoon is divided into brigades of 12 people, then again 2 people will not fit into any brigade. What is the minimum number of soldiers that need to be added to the platoon so that it can be completely divided into brigades of 7 people and also into brigades of 12 people?
|
A platoon can be entirely divided into brigades of 7 and brigades of 12 if and only if the number of people in it is divisible by $7 \cdot 12=84$.
Remove two people from the platoon. Then the remaining people can be divided into brigades both ways, meaning their number is divisible by 84. Return the two removed people; to reach the next number divisible by 84, we need to add 82 more people.
|
82
|
Number Theory
|
olympiads
| null | null |
\(\boxed{82}\)
|
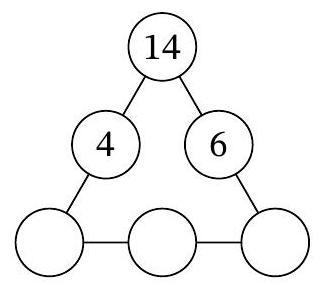
Problem 7.7. In three of the six circles of the diagram, the numbers 4, 14, and 6 are recorded. In how many ways can natural numbers be placed in the remaining three circles so that the products of the triples of numbers along each of the three sides of the triangular diagram are the same?
|
Let $a, b, c$ be the natural numbers in the three lower circles, from left to right. According to the condition, $14 \cdot 4 \cdot a = 14 \cdot 6 \cdot c$, i.e., $2a = 3c$. From this, it follows that $3c$ is even, and therefore $c$ is even. Thus, $c = 2k$ for some natural number $k$, and from the equation $2a = 3c$ it follows that $a = 3k$.
It must also hold that $14 \cdot 4 \cdot 3k = 3k \cdot b \cdot 2k$, which means $b \cdot k = 28$. Note that by choosing the number $k$, which is a natural divisor of 28, the natural numbers $a, b, c$ are uniquely determined. The number 28 has exactly 6 natural divisors: $1, 2, 4, 7, 14, 28$. Therefore, there are also 6 ways to place the numbers in the circles.
|
6
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{6}\)
|
Problem 8.2. The arithmetic mean of three two-digit natural numbers $x, y, z$ is 60. What is the maximum value that the expression $\frac{x+y}{z}$ can take?
|
From the condition, it follows that the sum of the numbers $x, y, z$ is $60 \cdot 3=180$. Then
$$
\frac{x+y}{z}=\frac{180-z}{z}=\frac{180}{z}-1 \leqslant \frac{180}{10}-1=17
$$
since $z \geqslant 10$. Note also that when $x=90, y=80, z=10$, the value 17 is achieved.
|
17
|
Algebra
|
olympiads
| null | null |
\(\boxed{17}\)
|
Problem 8.4. Find any solution to the puzzle
$$
\overline{A B C A}=182 \cdot \overline{C D}
$$
where $A, B, C, D$ are four different non-zero digits (the notation $\overline{X Y \ldots Z}$ means the decimal representation of the number).
As an answer, write the four-digit number $\overline{A B C D}$.
|
$\overline{A B C A}=1001 A+10 \cdot \overline{B C}$. Note that 1001 and 182 are divisible by 91, therefore, $10 \cdot \overline{B C}$ is also divisible by 91, i.e., $\overline{B C}=91$.
Substituting $B=9, C=1$ and dividing by 91, we get the equation $11 A=10+2 D$. On the left side of this equation, we have a number divisible by 11, and on the right side, an even two-digit number less than 30. Therefore, this number is 22, from which $A=2$ and $D=6$.
|
2916
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{2916}\)
|
Problem 8.5. In a race, several people participated, including Andrey, Dima, and Lёnya. No two participants of this race arrived at the same time.
- The number of people who arrived before Andrey is 2 times less than the number of people who arrived after him.
- The number of people who arrived before Dima is 3 times less than the number of people who arrived after him.
- The number of people who arrived before Lёnya is 4 times less than the number of people who arrived after him.
What is the smallest number of people that could have participated in the race?
|
Let $x$ be the number of people who ran before Andrey, then $2x$ people ran after him. We get that there were $3x+1$ participants in the race.
Let $y$ be the number of people who ran before Dima, then there were $4y+1$ participants in total.
Finally, let $z$ be the number of people who ran before Lenya, then there were $5z+1$ participants in total.
If we subtract 1 from the total number of runners, the result should be divisible by 3, 4, and 5. The smallest such number is 60, so there were at least 61 participants.
It remains to note that the condition could have been met with 61 participants. For example, if among them Andrey came in 21st, Dima in 16th, and Lenya in 13th.
|
61
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{61}\)
|
Problem 8.8. A computer can apply three operations to a number: "increase by 2", "increase by 3", "multiply by 2". The computer was given the number 1 and was made to try all possible combinations of 6 operations (each of these combinations is applied to the initial number 1). After how many of these combinations will the computer end up with an even number?
|
If the number was odd before the last operation, then one of the two operations "increase by 3" or "multiply by 2" will make it even, but the third will not. Similarly, if the number was even before the last operation, then one of the two operations "increase by 2" or "multiply by 2" will make it even, but the third will not.
Thus, the first 5 operations can be performed in any order - this gives $3^{5}$ options. To get an even result on the last operation, there are exactly 2 options, so the total number of combinations is $3^{2} \cdot 2=486$.
## 9th grade
|
486
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{486}\)
|
Problem 9.2. In the first hour of the shift, the master made 35 parts. Then he realized that, maintaining the current speed, he would have to stay an extra hour to complete the shift's plan. By increasing his speed by 15 parts per hour, he completed the plan half an hour before the end of the shift. How many parts should the master produce during the shift?
|
Let $N$ be the number of parts he still needs to manufacture. If he continued to make 35 parts per hour, he would finish in $\frac{N}{35}$ hours. When he sped up and started producing 50 parts per hour, he completed the work in $\frac{N}{50}$ hours.
From the condition, it follows that $\frac{N}{35}-\frac{N}{50}=1.5$, which means $\frac{3}{350} N=1.5$, from which we find $N=175$. Then the number of parts that need to be manufactured in one shift is $175+35=210$.
|
210
|
Algebra
|
olympiads
| null | null |
\(\boxed{210}\)
|
Problem 9.3. The farmer said: "I have $N$ rabbits. Long ears are exactly on 13 of them. And exactly 17 of them can jump far."
The traveler rightly noted: "Therefore, among your rabbits, there are at least 3 rabbits that simultaneously have long ears and can jump far."
What is the largest value that the number $N$ can take?
|
If $N \geqslant 28$, then the traveler is wrong: it is possible that the farmer had only 2 long-eared rabbits that can jump far. In addition to them, there were 11 long-eared rabbits that cannot jump far, and 15 rabbits without long ears that can jump far. The remaining $N-28$ rabbits neither have long ears nor can jump far.
If $N=27$, then the traveler is right. Indeed, from the condition, it follows that exactly 10 rabbits cannot jump far. Since 13 rabbits have long ears, at least $13-10=3$ of them both have long ears and can jump far.
|
27
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{27}\)
|
Problem 9.6. The teacher wrote a number on the board. Sasha decided to divide it by 102 with a remainder, and Masha - by 103. It turned out that the quotient obtained by Sasha and the remainder obtained by Masha add up to 20. What remainder did Sasha get? List all possible options.
|
Let $n$ be the number on the board, divide it by 102 and by 103 with remainders:
$$
n=102 a+b ; \quad n=103 c+(20-a)
$$
Subtract the second equation from the first:
$$
0=103(a-c)+(b-20)
$$
From this, it follows that $b-20$ is divisible by 103. Since $0 \leqslant b \leqslant 101$, we get that $b=20$.
Notice also that, for example, for the number $n=122$, the remainder $b=20$ is indeed possible.
|
20
|
Number Theory
|
olympiads
| null | null |
\(\boxed{20}\)
|
Problem 10.2. How many real numbers $x$ exist such that the value of the expression $\sqrt{123-\sqrt{x}}$ is an integer?
|
From the condition, it follows that the value $s=123-\sqrt{x} \leqslant 123$ is a square of an integer. Since $11^{2}<123<12^{2}$, this value can take one of 12 values $0^{2}$, $1^{2}, 2^{2}, \ldots, 11^{2}$. And for each of these 12 values of $s$, there is a unique value of $x=(123-s)^{2}$ (obviously, all these values of $x$ are distinct).
|
12
|
Algebra
|
olympiads
| null | null |
\(\boxed{12}\)
|
Problem 10.4. Consider the sequence
$$
a_{n}=\cos (\underbrace{100 \ldots 0^{\circ}}_{n-1})
$$
For example, $a_{1}=\cos 1^{\circ}, a_{6}=\cos 100000^{\circ}$.
How many of the numbers $a_{1}, a_{2}, \ldots, a_{100}$ are positive?
|
Note that for an integer $x$ divisible by 40, the cosines of the angles $x^{\circ}$ and $10 x^{\circ}$ coincide, since the difference between these angles $9 x^{\circ}$ is divisible by $360^{\circ}$. Therefore, $\cos \left(\left(10^{k}\right)^{\circ}\right)=$ $\cos \left(\left(10^{k+1}\right)^{\circ}\right)$ for all $k \geqslant 3$.
It is clear that $\cos \left(1^{\circ}\right)>0, \cos \left(10^{\circ}\right)>0, \cos \left(100^{\circ}\right)<0$, and subsequently $0<\cos \left(1000^{\circ}\right)=\cos \left(10000^{\circ}\right)=\ldots=$ $\cos \left(\left(10^{99}\right)^{\circ}\right)$. Thus, among our numbers, exactly 99 are positive.
|
99
|
Number Theory
|
olympiads
| null | null |
\(\boxed{99}\)
|
1. Let's divide the sequence of natural numbers into groups:
$(1),(2,3),(4,5,6)(7,8,9,10), \ldots$
Denote $S_{n}$ as the sum of the $n$-th group of numbers. Find $S_{16}-S_{4}-S_{1}$.
|
Note that in the $n$-th group there are $n$ terms and the first one is $\frac{n(n-1)}{2}+$ 1. The last term of the $n$-th group is $\frac{n(n-1)}{2}+1+(n-1)=\frac{n^{2}+n}{2}$. Therefore, $S_{n}=\left(\frac{n(n-1)}{2}+1+\frac{n(n+1)}{2}\right) \cdot \frac{n}{2}=\frac{n\left(n^{2}+1\right)}{2}$. Hence, $S_{16}-S_{4}-S_{1}=$ $2056-34-1=2021$
|
2021
|
Number Theory
|
olympiads
| null | null |
\(\boxed{2021}\)
|
# 5.1. Condition:
Polina came to the cafeteria and saw that 2 puff pastries cost 3 times more than 2 pies. Polina didn't have enough money for 2 puff pastries, but she did have enough for 1 pie and 1 puff pastry. After the purchase, she wondered how many times more money she spent buying 1 puff pastry and 1 pie instead of 2 pies. Help Polina answer this question.
|
## Solution.
2 puff pastries are 3 times more expensive than 2 pies, so one puff pastry is 3 times more expensive than one pie, which means one puff pastry costs as much as 3 pies. Therefore, 1 puff pastry and 1 pie cost as much as 4 pies. Then they are 2 times more expensive than 2 pies.
|
2
|
Algebra
|
olympiads
| null | null |
\(\boxed{2}\)
|
9.1. If the discriminant of the quadratic polynomial $f(x)=a x^{2}+2 b x+c$ is subtracted from the discriminant of the quadratic polynomial $g(x)=(a+1) x^{2}+2(b+2) x+c+4$, the result is 24. Find $f(-2)$.
|
We have: $D_{1}-D_{2}=4\left(b^{2}-a c-(b+2)^{2}+(a+1)(c+4)\right)=4(-4 b+4 a+c)=$ $4 f(-2)$.
Comment: Correct answer without justification - 0 points.
|
6
|
Algebra
|
olympiads
| null | null |
\(\boxed{6}\)
|
11.1. The numbers $2^{2019}$ and $5^{2019}$ are written consecutively. How many digits are written in total?
|
Let the number $2^{2019}$ contain $\mathrm{m}$ digits, and the number $5^{2019}$ contain $\mathrm{n}$ digits. Then the following inequalities hold: $10^{\mathrm{m}-1}<2^{2019}<10^{\mathrm{m}}, 10^{\mathrm{n}-1}<5^{2019}<10^{\mathrm{n}}$ (the inequalities are strict because the power of two or five is not equal to the power of ten). Multiplying these inequalities, we get: $10^{\mathrm{m}+\mathrm{n}-2}<10^{2019}<10^{\mathrm{m}+\mathrm{n}}$. From this, it follows that the exponent 2019 is between $\mathrm{m}+\mathrm{n}-2$ and $\mathrm{m}+\mathrm{n}$, so $2019=\mathrm{m}+\mathrm{n}-1$ and $\mathrm{m}+\mathrm{n}=2020$. This means that a total of 2020 digits have been written.
|
2020
|
Number Theory
|
olympiads
| null | null |
\(\boxed{2020}\)
|
10.1. Find at least one four-digit number that has the following property: if the sum of all its digits is multiplied by the product of all its digits, the result is 3990. (I. Rubanov)
|
Note that $3990=2 \cdot 3 \cdot 5 \cdot 7 \cdot 19=1 \cdot 6 \cdot 5 \cdot 7 \cdot 19$ and $6+5+7+1=19$. Therefore, any four-digit number that contains one 1, one 6, one 5, and one 7 will work, for example, 1567.
Comment. To receive full credit, it is sufficient to provide any correct example.
|
1567
|
Number Theory
|
olympiads
| null | null |
\(\boxed{1567}\)
|
1. How many 4-digit numbers exist where the digit in the thousands place is greater than the digit in the hundreds place?
|
The digit in the thousands place can take one of 9 possible values: $1,2,3, \ldots, 9$ (we cannot take 0, since the number is four-digit). For each of these options, we can specify the corresponding number of options for the hundreds digit: 1, $2,3, \ldots, 9$. That is, there are a total of 45 options. The other two digits are arbitrary (10 options each), so we get the answer: $45 \cdot 10 \cdot 10=4500$ options.
|
4500
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{4500}\)
|
2.1. Sasha solved the quadratic equation $3 x^{2}+b x+c=0$ (where $b$ and $c$ are some real numbers). In his answer, he got exactly one root: $x=-4$. Find $b$.
|
By Vieta's theorem $x_{1}+x_{2}=-b / 3$. In our case $x_{1}=x_{2}=-4$, hence $-b / 3=-8$ and $b=24$.
Remark. Another solution can be obtained by noticing that the equation should reduce to a perfect square $3(x+4)^{2}=0$.
|
24
|
Algebra
|
olympiads
| null | null |
\(\boxed{24}\)
|
3.1. Find the sum
$$
\sqrt[7]{(-7)^{7}}+\sqrt[8]{(-8)^{8}}+\sqrt[9]{(-9)^{9}}+\ldots+\sqrt[100]{(-100)^{100}}
$$
(Each term is of the form $\left.\sqrt[k]{(-k)^{k}}\right)$
|
Note that $\sqrt[k]{(-k)^{k}}$ equals $k$ when $k$ is even, and equals $-k$ when $k$ is odd. Therefore, our sum is $-7+8-9+10-\ldots-99+100=(-7+8)+(-9+10)+\ldots+(-99+100)$. In the last expression, there are 47 parentheses, each of which equals 1.
|
47
|
Algebra
|
olympiads
| null | null |
\(\boxed{47}\)
|
Problem 1. Vasya thought of a two-digit number, then added the digit 1 to the left of it, and the digit 8 to the right, which increased the number by 28 times. What number could Vasya have thought of? (Find all options and prove that there are no others.)
|
Let Vasya have thought of the number $n$. When the digit 8 is appended to the right, it turns into the number $10 n+8$, and when the digit 1 is appended to the left, it increases by 1000, therefore
$$
\begin{gathered}
10 n+1008=28 n \\
18 n=1008 \\
n=56
\end{gathered}
$$
## Criteria
4 6. A complete and justified solution is provided.
In the absence of a correct solution, the highest applicable criterion from those listed below is used:
3 p. The equation is correctly set up, but an arithmetic error is made in solving it.
2 6. The correct answer is provided, but there is no justification.
06. The problem is not solved or is solved incorrectly.
|
56
|
Number Theory
|
olympiads
| null | null |
\(\boxed{56}\)
|
9.3. Solve the equation:
$1+\frac{3}{x+3}\left(1+\frac{2}{x+2}\left(1+\frac{1}{x+1}\right)\right)=x$.
#
|
# Solution.
$1+\frac{1}{x+1}=\frac{x+2}{x+1}$, therefore the given equation is equivalent to the equation $1+\frac{3}{x+3}\left(1+\frac{2}{x+1}\right)=x$ under the condition that $\mathrm{x} \neq-2$. Proceeding similarly, we get that $1+\frac{3}{x+3}=x$, where $\mathrm{x} \neq-2$ and $\mathrm{x} \neq-3$. The roots of this equation are the numbers 2 and -2, so the only root of the original equation is the number 2.
## Grading Criteria
- Only the correct answer is provided - 1 point.
- The correct solution process, but the extraneous root is not discarded - 3 points.
|
2
|
Algebra
|
olympiads
| null | null |
\(\boxed{2}\)
|
Problem 4.2. Petya took half of the candies from the box and put them in two pockets. Deciding that he took too many, Petya took out 6 candies from each pocket and put them back into the box. By how many more candies did the box have than Petya's pockets?
|
Let $x$ be the number of candies in one of Petya's pockets before he returned some of the candies to the box. At that moment, there were $2 x$ candies in the box.
After Petya took out 6 candies from each pocket, he had
$$
(x-6)+(x-6)=2 x-12 \text{ candies }
$$
and there were $2 x+12$ candies in the box.
Thus, there were $(2 x+12)-(2 x-12)=24$ more candies in the box than Petya had.
|
24
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{24}\)
|
1.1. For what least natural value of \( b \) does the equation
$$
x^{2}+b x+25=0
$$
have at least one root?
|
The equation has at least one root if and only if the discriminant $D=b^{2}-4 \cdot 25=$ $=b^{2}-100$ is greater than or equal to 0. For positive $b$, this condition is equivalent to the condition $b \geqslant 10$.
|
10
|
Algebra
|
olympiads
| null | null |
\(\boxed{10}\)
|
2.1. Every month Ivan pays a fixed amount from his salary for a mortgage, and the remaining part of the salary is spent on current expenses. In December, Ivan paid $40 \%$ of his salary for the mortgage. In January, Ivan's salary increased by $9 \%$. By what percentage did the amount spent on current expenses increase in January (compared to December)?
|
Let Ivan's December salary be $100 r$. Then Ivan paid $40 r$ for the mortgage, and in December, he spent $60 r$ on current expenses. In January, Ivan's salary was $109 r$, so he spent $109 r - 40 r = 69 r$ on current expenses. Thus, the amount spent on current expenses increased by $9 r$, which is $\frac{9}{60}$ of the December amount or 15 percent.
|
15
|
Algebra
|
olympiads
| null | null |
\(\boxed{15}\)
|
4.1. In the product
$$
24^{a} \cdot 25^{b} \cdot 26^{c} \cdot 27^{d} \cdot 28^{e} \cdot 29^{f} \cdot 30^{g}
$$
the seven exponents $a, b, c, d, e, f, g$ were replaced by the numbers $1, 2, 3, 5, 8, 10, 11$ in some order. Find the maximum number of zeros that the decimal representation of this product can end with.
|
The prime factor 5 enters the factorization of this product with multiplicity $2 b+g$, so there are no more than $2 b+g$ zeros in this product. Since $b \leqslant 11$ (the largest of the given exponents) and $b+g \leqslant 11+10$ (the sum of the two largest of the given exponents), then $2 b+g \leqslant 11+11+10=32$.
On the other hand, for example, the product $24^{8} \cdot 25^{11} \cdot 26^{1} \cdot 27^{2} \cdot 28^{3} \cdot 29^{5} \cdot 30^{10}$ ends with exactly 32 zeros, since the prime number 5 enters the factorization of this product with multiplicity $2 \cdot 11+10=32$, and the prime number 2 enters the factorization of this product with multiplicity $3 \cdot 8+1+3+10>32$.
|
32
|
Number Theory
|
olympiads
| null | null |
\(\boxed{32}\)
|
4. Every day, from Monday to Friday, the old man went to the blue sea and cast his net into the water. Each day, the net caught no more fish than the previous day. In total, over the five days, the old man caught exactly 100 fish. What is the smallest total number of fish he could have caught on the three days - Monday, Wednesday, and Friday?
|
Estimation. On Tuesday and Thursday, the old man caught no more fish than on Monday and Wednesday, so over the specified three days, he caught no less than half of 100, which is no less than 50 fish.
Example. If the old man caught 25 fish each of the first four days and caught nothing on Friday, the conditions of the problem are met, and exactly 50 fish were caught over the specified three days.
|
50
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{50}\)
|
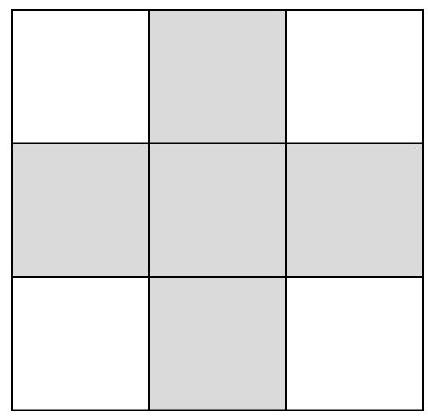
Problem 4.3. How many rectangles exist on this picture with sides running along the grid lines? (A square is also a rectangle.)

|
In a horizontal strip $1 \times 5$, there are 1 five-cell, 2 four-cell, 3 three-cell, 4 two-cell, and 5 one-cell rectangles. In total, $1+2+3+4+5=15$ rectangles.
In a vertical strip $1 \times 4$, there are 1 four-cell, 2 three-cell, 3 two-cell, and 4 one-cell rectangles. In total, $1+2+3+4=10$ rectangles. At the same time, one one-cell rectangle at the intersection of the strips is counted twice (and only it is). Therefore, the answer to the problem is the number $15+10-1=24$.
|
24
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{24}\)
|
Problem 5.3. A cuckoo clock is hanging on the wall. When a new hour begins, the cuckoo says "cuckoo" a number of times equal to the number the hour hand points to (for example, at 19:00, "cuckoo" sounds 7 times). One morning, Maxim approached the clock when it was 9:05. He started turning the minute hand until he advanced the clock by 7 hours. How many times did "cuckoo" sound during this time?

|
The cuckoo will say "cuckoo" from 9:05 to 16:05. At 10:00 it will say "cuckoo" 10 times, at 11:00 - 11 times, at 12:00 - 12 times. At 13:00 (when the hand points to the number 1) "cuckoo" will sound 1 time. Similarly, at 14:00 - 2 times, at 15:00 - 3 times, at 16:00 - 4 times. In total
$$
10+11+12+1+2+3+4=43
$$
|
43
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{43}\)
|
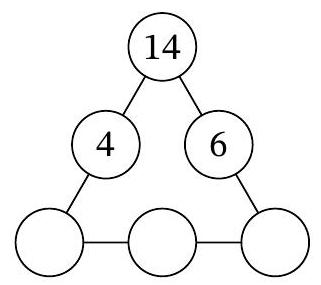
Problem 7.7. In three of the six circles of the diagram, the numbers 4, 14, and 6 are recorded. In how many ways can natural numbers be placed in the remaining three circles so that the products of the triples of numbers along each of the three sides of the triangular diagram are the same?
|
Let $a, b, c$ be the natural numbers in the three lower circles, from left to right. According to the condition, $14 \cdot 4 \cdot a = 14 \cdot 6 \cdot c$, i.e., $2a = 3c$. From this, it follows that $3c$ is even, and therefore $c$ is even. Thus, $c = 2k$ for some natural number $k$, and from the equation $2a = 3c$ it follows that $a = 3k$.
It must also hold that $14 \cdot 4 \cdot 3k = 3k \cdot b \cdot 2k$, which means $b \cdot k = 28$. Note that by choosing the number $k$, which is a natural divisor of 28, the natural numbers $a, b, c$ are uniquely determined. The number 28 has exactly 6 natural divisors: $1, 2, 4, 7, 14, 28$. Therefore, there are also 6 ways to place the numbers in the circles.
|
6
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{6}\)
|
2. The plane departed from Perm on September 28 at noon and arrived in Kirov at 11:00 AM (all departure and arrival times mentioned in the problem are local). At 7:00 PM the same day, the plane departed from Kirov to Yakutsk and arrived there at 7:00 AM. Three hours later, it departed from Yakutsk to Perm and returned there at 11:00 AM on September 29. How much time did the plane spend in the air? Answer: 12 hours.
|
# Solution.
The plane was absent in Perm for 23 hours. Out of these, it was stationed in Kirov for 8 hours (from 11 to 19) and for 3 hours in Yakutsk. In total, out of these 23 hours, it was stationed $8+3=11$ (hours), i.e., the plane was in the air for $23-11=12$ (hours).
## Grading Criteria.
- Correct solution -7 points.
- Correct answer without justification -2 points.
|
12
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{12}\)
|
7.2 Vasya saved 80 rubles in 5-kopeck coins. To pay off a debt of 25 rubles to his friend, he started counting the coins, but got confused and decided to use a balance scale. How can he separate the required amount in 4 weighings, if he has no weights?
|
2 Vasya has saved 80 rubles in 5-kopeck coins. To pay off a debt of 25 rubles to his friend, he started counting the coins but got confused and decided to use a balance scale. How can he separate the required amount in 4 weighings, if he has no weights?
Hint: In the first weighing, Vasya divides all the coins into two equal-weight piles and gets two piles of 40 rubles each. Then he similarly divides one of the 40-ruble piles into two equal parts. By repeating this process two more times, he will end up with two piles of 5 rubles and three piles of 10, 20, and 40 rubles. By combining the 5-ruble and 20-ruble piles, he will get the required amount.
|
25
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{25}\)
|
1.1. At the stadium, through the checkpoints numbered 1, 2, 3, and 4, an equal number of fans entered. They then passed through several more checkpoints, moving along the arrows, and at the fork, the fans were evenly distributed. At checkpoint 7, 15 people passed the control.
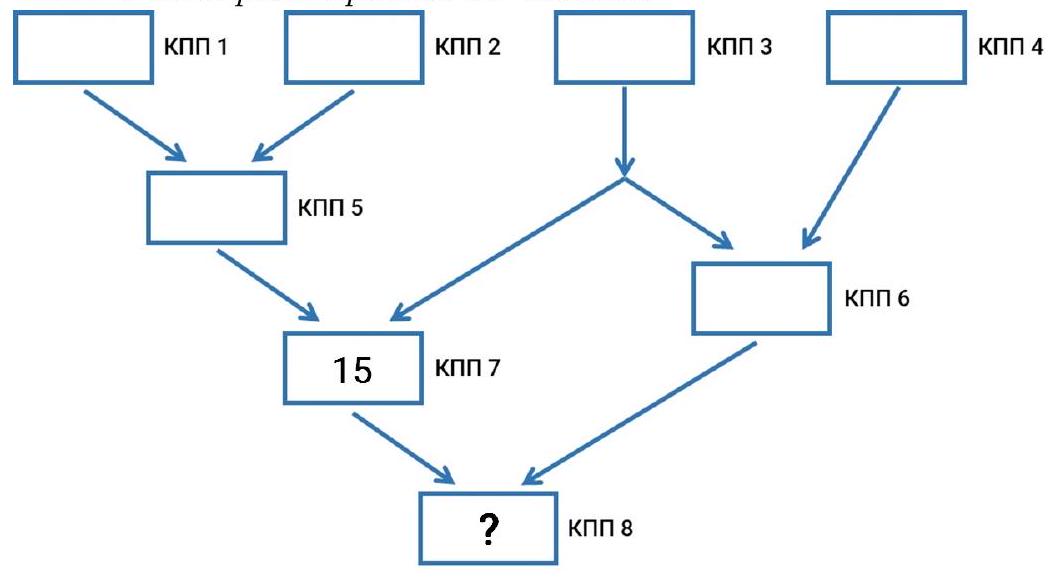
How many people passed through checkpoint 8?
Checkpoint (control and pass point) - a place where stadium staff check fans for tickets and prohibited items.
|
Let $2x$ people pass through each of the first four checkpoints. Then, through checkpoint 7, $2x$ people passed from the first two checkpoints and $x$ from the third, totaling $5x=15$ people, from which $x=3$. Therefore, each of the first four checkpoints had 6 people, and checkpoint 8 was passed by everyone who entered through the first four checkpoints, which is 24 people.
|
24
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{24}\)
|
3.1. A gardener grows white and red flowers: peonies and roses. In his garden, there are 301 stems, among which 135 are roses and 182 are red flowers. What is the smallest number of red peonies that can grow in the gardener's garden?
|
Estimation: The number of red peonies is the difference between the number of red flowers and the number of red roses. The number of red roses is no more than the total number of roses, i.e., no more than 135. Therefore, the number of red peonies is no less than $182-135=47$.
Let's provide an example where the conditions of the problem are met, and the number of red peonies is exactly 47. Suppose there are 47 red peonies, 135 red roses, 0 white roses, and 119 white peonies.
|
47
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{47}\)
|
# 1. Option 1.
Find the value of the expression $101+102-103-104+105+106-107-108+\ldots-619$?
|
Subtract and add the number 620 at the end of the expression. Then the numbers from 101 to 620 will be divided into $(620-100): 4=130$ quartets. And in each quartet, the sum of the numbers will be equal to -4. Then the value of the expression will be equal to $(101+102-103-104)+(105+106-107-108)+\ldots-619-620)+620=$ $130(-4)+620=100$.
|
100
|
Algebra
|
olympiads
| null | null |
\(\boxed{100}\)
|
Problem 4.2. In class 4A, each child has no fewer than 11 classmates and no fewer than 13 female classmates. What is the smallest number of children that can study in this class?
|
It is not difficult to verify that a class consisting of 12 boys and 14 girls satisfies the condition of the problem. Now let's prove that it cannot be less.
It is clear that there are both boys and girls in the class. Each boy in the class has at least 11 classmates, so there must be at least 12 boys in total. Each girl in the class has at least 13 female classmates, so there must be at least 14 girls in total. Therefore, there are at least $12+14=26$ children in the class.
|
26
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{26}\)
|
Problem 8.2. The numbers from 1 to 9 were placed in the cells of a $3 \times 3$ table such that the sum of the numbers on one diagonal is 7, and on the other diagonal is 21. What is the sum of the numbers in the five shaded cells?
|
Note that 7 can be represented uniquely as the sum of numbers from 1 to 9 - this is $1+2+4=7$.
Let's look at the other diagonal with a sum of 21. The largest possible value of the sum in it is $9+8+4=21$ (since the number in the central cell is no more than 4). Therefore, it must contain the numbers $9,8,4$.
Thus, the number 4 is in the central cell, and the numbers 1, 2, 8, and 9 are at the corners. Now it is not difficult to find the sum of the numbers in the shaded cells: $3+4+5+6+7=25$.
|
25
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{25}\)
|
3. There are more than 20 but fewer than 30 people in the class, and everyone has a different birthday. Petya said: "There are twice as many people older than me as there are younger than me in the class." Katya said: "There are three times fewer people older than me as there are younger than me in the class." How many people are in the class if Petya and Katya are both correct?
|
From Petya's words, it is clear that without him, the number of students in the class is a multiple of 3 (2 parts + 1 part). That is, together with him, there can be 22, 25, or 28 people in the class. Similarly, from Katya's words, it is clear that without her, the number of students in the class is a multiple of 4. The numbers that fit are 21, 25, 29. Since both statements are true, the number that satisfies both conditions is 25.
Grading criteria: Correct answer with verification - 1 point.
If the solution is by enumeration and one of the cases from 21 to 29 is missed without explanation, then 1 point.
Correct answer with all necessary explanations - 7 points.
|
25
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{25}\)
|
2. In the pop ensemble "Sunshine," everyone plays either the violin or the double bass. The average age of those who play the violin is 22 years, and those who play the double bass is 45 years. Igor changed his instrument and started playing the violin instead of the double bass. As a result, the average age of those who play the violin increased by 1 year, and the average age of those who play the double bass also increased by 1 year. How many people are in the ensemble "Sunshine"? Answer: 23.
|
Let $x$ be the number of people who play the contrabass, excluding Igor, and $y$ be the number of people who play the violin (also excluding Igor).
From the condition, it follows that the total age of those who play the contrabass was initially equal to: $(x+1) \cdot 45$, and when Igor changed the instrument, it became equal to $x \cdot 46$.
Then Igor's age is $(x+1) \cdot 45 - x \cdot 46 = 45 - x$.
Similarly, we get that Igor's age is $23 \cdot (y+1) - 22 \cdot y = y + 23$.
Then $45 - x = y + 23$, from which $x + y = 22$ is the number of pirates without Igor, and with Igor - 23.
|
23
|
Algebra
|
olympiads
| null | null |
\(\boxed{23}\)
|
8. 8.1. How many increasing arithmetic progressions of 22 different natural numbers exist, in which all numbers are no greater than 1000?
|
## Solution.
Consider the 22nd term of each such progression, it will have the form $a_{22}=a_{1}+21d$. This means that $a_{1}$ and $a_{22}$ will have the same remainders when divided by 21. Each pair of numbers not exceeding 1000, giving the same remainders when divided by 21, defines one of the required progressions, since to construct a progression it is sufficient to divide the segment between $a_{1}$ and $a_{22}$ on the number line into 21 equal parts. Let's find the number of such pairs. Since $1000=21 \cdot 47+13$, 13 remainders occur 48 times and 8 remainders 47 times. Then the number of the required progressions will be equal to $13 \cdot C_{48}^{2}+8 \cdot C_{47}^{2}=$ $\frac{13 \cdot 48 \cdot 47}{2}+\frac{8 \cdot 47 \cdot 46}{2}=23312$.
|
23312
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{23312}\)
|
2. Indicate the smallest number ending in 37 with the sum of its digits equal to 37 and divisible by 37.
|
The number is the smaller, the fewer digits are required to write it. Two digits - these are the last two digits, their sum is 10. Therefore, the sum of the other digits is 27, and there are at least three of them, since the largest digit is 9. Thus, the number 99937 satisfies three of the four requirements. It remains to check that it is divisible by
|
99937
|
Number Theory
|
olympiads
| null | null |
\(\boxed{99937}\)
|
4. In the rebus
$$
\mathbf{K}\mathbf{O}>\mathbf{H}>\mathbf{A}>\mathbf{B}>\mathbf{U}>\mathbf{P}>\mathbf{y}>\mathbf{C}
$$
different letters represent different digits. How many solutions does the rebus have?
|
From the rebus, it follows that $\mathbf{P}>\mathbf{O}>\mathbf{P}$. This cannot be! Evaluation. 7 points for the correct solution.
|
0
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{0}\)
|
Problem 4. There are 10 identical swimming pools and two hoses with different pressures. It is known that the first hose fills a pool 5 times faster than the second. Petya and Vasya each started filling 5 pools, Petya with the first hose, and Vasya with the second. It is known that Petya finished an hour earlier. How long did it take Vasya to fill his 5 pools?
Answer: 1 hour 15 minutes.
|
Let Petya fill one pool in time $x$, then Vasya fills one pool in time $5 x$ (since the second hose fills one pool five times slower).
Then Petya will fill his five pools in time $5 x$, and Vasya his in $25 x$.
We get the equation $25 x-5 x=1$, from which $x=3$ min. Then Vasya will fill his pools in $25 x=25 \cdot 3=75$ min $=1$ hour 15 min.
## Criteria
## 1 p. Only the correct answer without justification.
3 p. The time to fill one pool by any hose is correctly found.
4 p. The correct answer and justification are provided.
|
1
|
Algebra
|
olympiads
| null | null |
\(\boxed{1}\)
|
2. For what least natural $n$ do there exist such natural $a$ and $b$ that
$$
\text { GCD }(a, b)=999 \text { and } \text{LCM}(a, b)=n!
$$
(here $n!=1 \cdot 2 \cdot \ldots \cdot n)$ ?
|
For what smallest natural $n$ do there exist such natural $a$ and $b$ that
$$
\text { GCD }(a, b)=999 \text { and } \text{LCM}(a, b)=n!
$$
(Here $n!=1 \cdot 2 \cdot \ldots \cdot n) ?$
ANSWER. $n=37$.
SOLUTION. Since $\text{LCM}(a, b)$ is divisible by $\text{GCD}(a, b)=999=27 \cdot 37$, and the number 37 is prime, $n \geqslant 37$. On the other hand, for $n=37$ the numbers $a=37!, b=999$ are suitable.
|
37
|
Number Theory
|
olympiads
| null | null |
\(\boxed{37}\)
|
5. Vova has 19 math grades in his journal, all twos and threes, and the first four grades are twos. It turned out that among the quartets of consecutive grades, all 16 possible combinations of four twos and threes are present. What are Vova's last four grades?
|
Vova has 19 math grades in his journal, all twos and threes, and the first four grades are twos. It turned out that among the quartets of consecutive grades, all 16 possible combinations of four twos and threes are present. What are Vova's last four grades?
ANSWER. 3222.
SOLUTION. Note that there are exactly 16 quartets of consecutive grades in a string of 19 grades, meaning each combination appears exactly once. After the first four twos, there must be a three, otherwise the combination of four twos would appear twice. Therefore, after the combination 3222, neither 2 nor 3 can follow, as in both cases, a combination that has already appeared would reappear. Thus, the combination 3222 must be at the end of the string.
|
3222
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{3222}\)
|
7.2. There are 9 cards with numbers $1,2,3,4,5,6,7,8$ and 9. What is the maximum number of these cards that can be laid out in some order in a row so that on any two adjacent cards, one of the numbers is divisible by the other?
|
Note that it is impossible to lay out all 9 cards in a row as required. This follows from the fact that each of the cards with numbers 5 and 7 can only have one neighbor card with the number 1. Therefore, both cards 5 and 7 must be at the edges, and the card with the number 1 must be adjacent to each of them, which is impossible.
It is possible to select 8 cards and arrange them in a row according to the requirements of the problem, for example: $9,3,6,2,4,8,1,5$.
Comment: Proof that it is impossible to lay out all the cards - 4 points.
Any correct example of arranging 8 cards - 3 points.
|
8
|
Number Theory
|
olympiads
| null | null |
\(\boxed{8}\)
|
1. Find the smallest number that contains only the digits 2 and 3 in equal quantities, and is divisible by 2 and 3.
|
Sketch of the solution. If a number is divisible by 3, then the sum of its digits is divisible by 3, which means the number of twos is a multiple of three, and thus, there must be at least three twos. Therefore, the desired number is a six-digit number. Since it is divisible by 2, it ends in 2. The number is smaller the smaller the leading digits are, hence the answer.
Criteria. Correct answer without justification: 2 points.
|
223332
|
Number Theory
|
olympiads
| null | null |
\(\boxed{223332}\)
|
1. There are candies in five bags. The first has 2, the second has 12, the third has 12, the fourth has 12, and the fifth has 12. Any number of candies can be moved from any bag to any other bag. What is the minimum number of moves required to ensure that all bags have an equal number of candies?
|
There are 50 candies in total and they should be 10 each. In four bags, there are 12 each, which is more than 10, and these bags participate in the redistributions to reduce to 10. Therefore, there are no fewer than 4 redistributions.
From the second to the fifth bag, two candies each go to the first.
Criteria. 2 points for an example of redistributions. 5 points for the estimate.
|
4
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{4}\)
|
3. There are seven red cubes, three blue ones, and nine green ones. Ten cubes were placed in a gift bag. In how many different ways could this have been done?
|
Let's put red cubes into the bag (8 ways from 0 to 7), now we place the blue cubes (4 ways from 0 to 3). Add the necessary number of green cubes (1 way). In total, $8 \times 4=32$.
One operation is impossible: 10 green. Therefore, there is one fewer way.
|
31
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{31}\)
|
8.4 The sequence of numbers $\mathrm{a}_{1}, \mathrm{a}_{2}, \mathrm{a}_{3}, \ldots, \mathrm{a}_{\mathrm{n}}, \ldots$ satisfies the relations $\mathrm{a}_{\mathrm{n}}=\mathrm{a}_{\mathrm{n}-1} \cdot \mathrm{a}_{\mathrm{n}-3}$ for $\mathrm{n}=4,5,6, \ldots$ Find $\mathrm{a}_{2019}$ if it is known that $\mathrm{a}_{1}=1, \mathrm{a}_{2}=1$, $\mathrm{a}_{3}=-1$
|
It is clear that all members of this sequence are equal to $\pm 1$. We find:
$$
\begin{aligned}
& a_{n}=\left(a_{n-1}\right) \cdot a_{n-3}=\left(a_{n-2} \cdot a_{n-4}\right) \cdot a_{n-3}=\left(a_{n-2}\right) \cdot a_{n-4} \cdot a_{n-3}= \\
& =\left(a_{n-3} \cdot a_{n-4}\right) \cdot a_{n-4} \cdot a_{n-3}=a_{n-3}^{2} \cdot a_{n-4} \cdot a_{n-5}=a_{n-4} \cdot a_{n-5}= \\
& =\left(a_{n-4}\right) \cdot a_{n-5}=\left(a_{n-5} \cdot a_{n-7}\right) \cdot a_{n-5}=a_{n-5}^{2} \cdot a_{n-7}=a_{n-7}
\end{aligned}
$$
That is, the sequence is periodic with a period of 7. Therefore,
$$
\mathrm{a}_{2019}=\mathrm{a}_{288 \cdot 7+3}=\mathrm{a}_{3}=-1
$$
|
-1
|
Algebra
|
olympiads
| null | null |
\(\boxed{-1}\)
|
9.2. In the basket, there are oranges and bananas. If you add as many oranges as there are currently bananas (in pieces), then the percentage of oranges
will be twice as much as it would be if you added as many bananas as there are currently oranges. What is the current percentage of oranges in the basket?
|
Let $a$ be the number of oranges, and $b$ be the number of bananas in the basket. If we add as many oranges as there are currently bananas, then there will be $a+b$ oranges out of $a+2b$ fruits, and the proportion of oranges will be $(a+b)/(a+2b)$. If we add as many bananas as there are currently oranges, then there will be $a$ oranges among $2a+b$ fruits, and the proportion of oranges will be $a/(2a+b)$. According to the problem, we have $(a+b)/(a+2b) = 2a/(2a+b)$. From this, we get $b^2 = ab$. Since there are more than zero bananas in the basket, $b = a$, meaning there are an equal number of bananas and oranges in the basket.
|
50
|
Algebra
|
olympiads
| null | null |
\(\boxed{50}\)
|
9.3. Find the value of the expression $x-\sqrt{2022 x}+2023$,
if $x-\sqrt{\frac{2022}{x}}=2023$.
|
Transform the condition $x-\sqrt{\frac{2022}{x}}=2023$ given that $x>0$. We get: $x^{2}-\sqrt{2022 x}=2023 x ; x^{2}-2022 x-x-\sqrt{2022 x}=0$;
$$
(x-\sqrt{2022 x})(x+\sqrt{2022 x})-(x+\sqrt{2022 x});(x-\sqrt{2022 x}-1)(x+
$$
$\sqrt{2022 x})=0$.
The second factor is positive for all $x>0$, which implies that $x-$ $\sqrt{2022 x}-1=0$, from which $x-\sqrt{2022 x}+2023=2024$.
|
2024
|
Algebra
|
olympiads
| null | null |
\(\boxed{2024}\)
|
1. Variant 1.
At the entrance to the amusement park, they sell children's and adult tickets. One children's ticket costs 600 rubles. Alexander bought 2 children's and 3 adult tickets, while Anna bought 3 children's and 2 adult tickets. It is known that Alexander paid 200 rubles more than Anna. How much did Alexander pay for the tickets in rubles?
|
## Solution.
Let $A$ be the cost of a children's ticket, and $B$ be the cost of an adult ticket. We calculate the difference $3B + 2A - 2B - 3A = B - A = 200$ rubles. This means the difference between the cost of an adult ticket and a children's ticket is 200 rubles. Then Alexander paid for the tickets $5 \cdot 600 + 3 \cdot 200 = 3600$ rubles.
|
3600
|
Algebra
|
olympiads
| null | null |
\(\boxed{3600}\)
|
2. Variant 1.
Given the set $A=\{1,2,3, \ldots, 1002\}$. Petya and Vasya are playing a game. Petya names a number $n$, and Vasya selects a subset from $A$ consisting of $n$ elements. Vasya wins if there are no two coprime numbers in the chosen subset; otherwise, Petya wins. What is the smallest $n$ that Petya should name to guarantee a win?
|
# Solution.
1) Estimation. Note that the set $A$ contains 501 even numbers. If Petya names $n \leq 502$, then Vasya can choose $n$ even numbers from this set and win.
2) Now we will show that for $n=502$, Vasya will lose. For this, it is sufficient to show that in the chosen subset, there will necessarily be two consecutive natural numbers. These numbers will be coprime.
We will divide all the numbers in the set $A$ into 501 pairs: 1 and 2, 3 and 4, 5 and 6, ..., 1001 and 1002. Then, by the pigeonhole principle, there will be at least two numbers that fall into the same pair. They are coprime, so Vasya loses.
|
502
|
Number Theory
|
olympiads
| null | null |
\(\boxed{502}\)
|
3. (7 points) The knightly tournament lasts exactly 7 days. By the end of the fourth day, Sir Lancelot had not yet faced one quarter of the total number of participants. And by this time, Sir Tristan had fought exactly one seventh of the knights that Sir Lancelot had faced. What is the minimum number of knights that could have participated in the tournament?
|
Let Lancelot not have fought with $x$ knights. Then the total number of knights is $4 x$, and Lancelot fought with $3 x-1$ knights (the total number minus $x$ and Lancelot himself). Then Tristan fought with $\frac{3 x-1}{7}$ knights. To find the smallest possible number of knights, we need to find the smallest $x$ such that $3 x-1$ is divisible by 7. The values $x=1,2,3,4$ do not work, but $x=5$ does. Thus, the smallest possible number of knights is 20.
Criteria. Any correct solution: 7 points.
For the absence of justification that there could indeed be exactly 20 knights, points are not deducted.
Only the correct answer is provided: 2 points.
|
20
|
Number Theory
|
olympiads
| null | null |
\(\boxed{20}\)
|
Problem 4.3. How many rectangles exist on this picture with sides running along the grid lines? (A square is also a rectangle.)
|
In a horizontal strip $1 \times 5$, there are 1 five-cell, 2 four-cell, 3 three-cell, 4 two-cell, and 5 one-cell rectangles. In total, $1+2+3+4+5=15$ rectangles.
In a vertical strip $1 \times 4$, there are 1 four-cell, 2 three-cell, 3 two-cell, and 4 one-cell rectangles. In total, $1+2+3+4=10$ rectangles. At the same time, one one-cell rectangle at the intersection of the strips is counted twice (and only it is). Therefore, the answer to the problem is the number $15+10-1=24$.
|
24
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{24}\)
|
Problem 5.3. A cuckoo clock is hanging on the wall. When a new hour begins, the cuckoo says "cuckoo" a number of times equal to the number the hour hand points to (for example, at 19:00, "cuckoo" sounds 7 times). One morning, Maxim approached the clock when it was 9:05. He started turning the minute hand until he advanced the clock by 7 hours. How many times did "cuckoo" sound during this time?

|
The cuckoo will say "cuckoo" from 9:05 to 16:05. At 10:00 it will say "cuckoo" 10 times, at 11:00 - 11 times, at 12:00 - 12 times. At 13:00 (when the hand points to the number 1) "cuckoo" will sound 1 time. Similarly, at 14:00 - 2 times, at 15:00 - 3 times, at 16:00 - 4 times. In total
$$
10+11+12+1+2+3+4=43
$$
|
43
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{43}\)
|
Problem 7.7. In three of the six circles of the diagram, the numbers 4, 14, and 6 are recorded. In how many ways can natural numbers be placed in the remaining three circles so that the products of the triples of numbers along each of the three sides of the triangular diagram are the same?
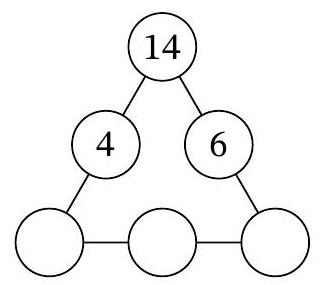
|
Let $a, b, c$ be the natural numbers in the three lower circles, from left to right. According to the condition, $14 \cdot 4 \cdot a = 14 \cdot 6 \cdot c$, i.e., $2a = 3c$. From this, it follows that $3c$ is even, and therefore $c$ is even. Thus, $c = 2k$ for some natural number $k$, and from the equation $2a = 3c$ it follows that $a = 3k$.
It must also hold that $14 \cdot 4 \cdot 3k = 3k \cdot b \cdot 2k$, which means $b \cdot k = 28$. Note that by choosing the number $k$, which is a natural divisor of 28, the natural numbers $a, b, c$ are uniquely determined. The number 28 has exactly 6 natural divisors: $1, 2, 4, 7, 14, 28$. Therefore, there are also 6 ways to place the numbers in the circles.
|
6
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{6}\)
|
9.6. Thirty girls - 13 in red dresses and 17 in blue dresses - were dancing in a circle around a Christmas tree. Later, each of them was asked if their right neighbor was in a blue dress. It turned out that those who answered correctly were only the girls standing between girls in dresses of the same color. How many girls could have answered affirmatively?
(R. Zhenodarov)
|
Consider any girl. The colors of the dresses of her left and right neighbors could have been: blue-blue, blue-red, red-blue, red-red. The girl answered "yes" in exactly the first two cases; therefore, she said "yes" exactly when her left neighbor was wearing a blue dress.
Thus, since exactly 17 girls had a left neighbor wearing a blue dress, the answer "yes" was given 17 times.
Remark: There are other (more complex) justifications for why exactly 17 girls in the circle answered "yes."
Comment: An answer alone (without justification, or obtained by considering specific cases of arrangement) -1 point.
For attempts at justification that do not consider all possible arrangements of the girls, no additional points are awarded.
|
17
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{17}\)
|
1. Variant 1.
Find the smallest natural number whose sum of digits is 47.
|
To find the smallest number, you need to get by with as few digits as possible. The largest digit is 9, so you can't do with fewer than 6 digits ( $5 \cdot 9<47$ ). We cannot put less than 2 in the first place, and by taking 2, the other five digits are uniquely determined: they are nines.
|
299999
|
Number Theory
|
olympiads
| null | null |
\(\boxed{299999}\)
|
2. Variant 1.
Athletes started in groups of 3 people with a delay between groups of several seconds. Petya, Vasya, and Kolya started simultaneously, and they were in the seventh trio from the beginning and the fifth trio from the end. How many athletes participated in the race?
|
After Petya, Kolya, and Vasya started, 4 more triples of athletes started. Then the total number of triples was $7+4=11$, i.e., a total of 33 athletes participated in the race.
|
33
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{33}\)
|
4. Variant 1.
The numbers $96, 28, 6, 20$ were written on the board. One of them was multiplied, another was divided, a third was increased, and a fourth was decreased by the same number. As a result, all the numbers became equal to one number. Which one?
|
Addition and multiplication increase numbers, while subtraction and division decrease them, so the two larger numbers have decreased, and the smaller ones have increased. Now let's consider the two middle numbers 20 and 28. It is clear that a number was subtracted from 28, and the same number was added to 20. There can be no other options, because if you add a number to 6 and multiply 20 by the same number, the numbers will not be equal. The numbers became equal, and $28-20=8$, so both became equal to the number 24. Note that $96: 24=4,28-24=4,20+4=24,6 \cdot 4=24$. Therefore, the required number is 24.
|
24
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{24}\)
|
# 7. Variant 1.
100 natural numbers are written in a circle. It is known that among any three consecutive numbers, there is an even number. What is the smallest number of even numbers that can be among the written numbers?
|
Consider any 3 consecutive numbers. Among them, there is an even number. Fix it, and divide the remaining 99 into 33 groups of 3 consecutive numbers. In each such group, there is at least one even number. Thus, the total number of even numbers is at least $1+33=34$. Such a situation is possible. Number the numbers in a circle. And the even numbers can be those with numbers $1,4,7, \ldots, 100$.
|
34
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{34}\)
|
# 7.1. (7 points)
Find the value of the expression
$$
\left(1+\frac{1}{2}\right)\left(1-\frac{1}{3}\right)\left(1+\frac{1}{4}\right)\left(1-\frac{1}{5}\right) \ldots\left(1+\frac{1}{2 m}\right)\left(1-\frac{1}{2 m+1}\right)
$$
|
Notice that
$$
\begin{array}{r}
\left(1+\frac{1}{2}\right)\left(1-\frac{1}{3}\right)=\frac{3}{2} \cdot \frac{2}{3}=1,\left(1+\frac{1}{4}\right)\left(1-\frac{1}{5}\right)=\frac{5}{4} \cdot \frac{4}{5}=1, \ldots \\
\left(1+\frac{1}{2 m}\right)\left(1-\frac{1}{2 m+1}\right)=\frac{2 m+1}{2 m} \cdot \frac{2 m}{2 m+1}=1
\end{array}
$$
Therefore, the value of the expression is 1.
#
|
1
|
Algebra
|
olympiads
| null | null |
\(\boxed{1}\)
|
1. The second term of an infinite decreasing geometric progression is 3. Find the smallest possible value of the sum $A$ of this progression, given that $A>0$.
|
Let the first term of the progression be $a$, and the common ratio be $q$. The sum of the progression $A$ is $\frac{a}{1-q}$. From the condition, we have $3=a q$, from which $a=3 / q$. Therefore, we need to find the minimum value of $A=\frac{3}{q(1-q)}$. Note that from the condition it follows: $0<q<1$. The number $A$ takes its minimum value when the denominator of the fraction $q(1-q)$ is maximized, but $\left(-q^{2}+q\right)$ has a maximum point at $q=1 / 2$, and the maximum value of $q(1-q)$ is $1 / 4$. Then the minimum possible value of $A=3 / 1 / 4=12$.
Comment. The sum $A$ is represented as a function of one variable - 3 points.
|
12
|
Algebra
|
olympiads
| null | null |
\(\boxed{12}\)
|
7.2. There are pan scales without weights and 11 visually identical coins, among which one may be counterfeit, and it is unknown whether it is lighter or heavier than the genuine coins (genuine coins have the same weight). How can you find at least 8 genuine coins in two weighings?
|
Let's divide the coins into three piles of three coins each. Compare pile 1 and pile 2, and then compare pile 2 and pile 3. If all three piles weigh the same, then all the coins in them are genuine, and we have found 9 genuine coins. Otherwise, one of the piles differs in weight from the others, and the counterfeit coin can only be in it. Then the genuine coins are in the other two piles plus the two remaining coins that we did not weigh.
|
9
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{9}\)
|
2. (7 points) There are apples in five boxes, with an equal number of apples in each. When 60 apples were taken out of each box, after that, the total number of apples left was the same as the number of apples that were originally in two boxes. How many apples were in each box?
Answer: 100.
|
In total, $60 \cdot 5=300$ apples were taken out, and this is equal to the number of apples that were in three boxes. Therefore, there were 100 apples in each box.
Criteria. Any correct solution: 7 points.
If it is not justified that there were 100 apples in each box, but it is verified that the condition is satisfied in this case: 4 points.
Correct answer without any explanation: 2 points.
|
100
|
Algebra
|
olympiads
| null | null |
\(\boxed{100}\)
|
1-0. The number 111123445678 is written on the board, and several digits (not all) need to be erased to get a number that is a multiple of 5. In how many ways can this be done?
|
The digits 6, 7, and 8 must be crossed out, and 5 must be kept (otherwise, the number will not be divisible by 5). Each digit before the five can be crossed out or not. There are two options for each of the digits 2 and 3 (cross out or not), three options for the digit 4 (do not cross out, cross out one, or cross out both), and five options for the ones (do not cross out any, cross out one, two, three, or all four). The deletions of different digits are independent events, so the obtained numbers should be multiplied: $5 \cdot 3 \cdot 2 \cdot 2=60$.
|
60
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{60}\)
|
2-0. The number $n$ is such that $8n$ is a 100-digit number, and $81n$ is a 102-digit number. What can the second digit from the beginning of $n$ be?
|
Since $8 n10^{101}$ (equality here is obviously impossible), it means $n>123 \cdot 10^{97}$. Therefore, the second digit from the beginning of the number $n$ is 2.
|
2
|
Number Theory
|
olympiads
| null | null |
\(\boxed{2}\)
|
4-0. Kisa and Busya came to the cafeteria during the break, where only muffins and doughnuts were sold, costing a whole number of rubles. Kisa bought 8 muffins and 3 doughnuts, spending less than 200 rubles, while Busya bought 4 muffins and 5 doughnuts, spending more than 150 rubles. Name the highest possible price of one muffin.
|
Let the price of a cake be $k$, and the price of a bun be $p$ rubles. Then $8 k+3 p<150$. Multiplying the first inequality by 5, and the second by 3, we get $40 k+15 p<1000, -12 k-15 p<-450$. Adding these inequalities: $28 k<550$, from which, taking into account the integer nature, $k \leqslant 19$.
Note that the case $k=19, p=15$ satisfies all conditions.
|
19
|
Algebra
|
olympiads
| null | null |
\(\boxed{19}\)
|
7-0. The number $n$ has exactly six divisors (including 1 and itself). They were arranged in ascending order. It turned out that the third divisor is seven times greater than the second, and the fourth is 10 more than the third. What is $n$?
|
If $n$ has six divisors, then either $n=p^{5}$ or $n=p \cdot q^{2}$ (where $p$ and $q$ are prime numbers). In the first case, $p=7$ (since the third divisor is seven times the second), but then the second condition is not satisfied.
Therefore, $n$ has two prime divisors (one of which is squared), and one of the prime factors is 7. Let the smallest divisors of $n$ be $1, p, 7p$, and $7p+10$. If $p=7$, then $7p+10=59$, and we get the answer 2891. If $p<7$, then $p=2$ (then $7p+10=24$, and such a number has more than six divisors). If $p=3$, then $7p+10=31$, and if $p=5$, then $7p+10=45$. In each of these cases, $n$ has more than two prime divisors.
|
2891
|
Number Theory
|
olympiads
| null | null |
\(\boxed{2891}\)
|
4. For numbers $a, b, c, d$, it is known that $a^{2}+b^{2}=1, c^{2}+d^{2}=1, a c+b d=0$. Calculate $a b+c d$.
|
Consider the equality: $(a c+b d)(a d+b c)=0$, since $a c+b d=0$.
We get $a^{2} c d+b^{2} c d+c^{2} a b+d^{2} a b=0$ or $\left(a^{2}+b^{2}\right) c d+\left(c^{2}+d^{2}\right) a b=0$.
Since $a^{2}+b^{2}=1$ and $c^{2}+d^{2}=1$ we obtain $a b+c d=0$.
|
0
|
Algebra
|
olympiads
| null | null |
\(\boxed{0}\)
|
1. Find the value of the expression $a^{3}+b^{3}+12 a b$, given that $a+b=4$.
|
$a^{3}+b^{3}+12 a b=(a+b)\left(a^{2}-a b+b^{2}\right)+12 a b=4\left(a^{2}-\right.$ $\left.a b+b^{2}\right)+12 a b=4 a^{2}+4 b^{2}+8 a b=4(a+b)^{2}=4 \cdot 16=64$
|
64
|
Algebra
|
olympiads
| null | null |
\(\boxed{64}\)
|
2. The boy went to the shooting range with his father. The father bought him 10 bullets. Later, the father took away one bullet for each miss and gave one additional bullet for each hit. The son fired 55 times, after which he ran out of bullets. How many times did he hit the target?
|
Each time the boy hit the target, the number of bullets he had remained the same (he used one and received one from his father). Each time the boy missed, the number of bullets he had decreased by 2 (he used one and his father took one). This means that the son missed $10: 2=5$ times out of 55 shots, so he hit 55 - 5 $=50$ times.
|
50
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{50}\)
|
Problem 5.3. Irina did poorly in math at the beginning of the school year, so she had 3 threes and 2 twos in her journal. But in mid-October, she pulled herself together and started getting only fives. What is the minimum number of fives Irina needs to get so that her average grade is exactly 4?
|
Let Irina need to get $x$ fives. Then the sum of her grades will be $3 \cdot 3+2 \cdot 2+5 x=5 x+13$, and the number of grades $-3+2+x=x+5$.
We get the equation
$$
\begin{aligned}
(5 x+13) & :(x+5)=4 \\
5 x+13 & =4(x+5) \\
5 x+13 & =4 x+20 \\
x & =7
\end{aligned}
$$
|
7
|
Algebra
|
olympiads
| null | null |
\(\boxed{7}\)
|
Problem 5.5. On some trees in the magical forest, coins grow. The number of trees that do not grow any coins at all is twice as many as the trees that grow three coins. On three trees, two coins grow, on four trees - four coins, and no tree grows more than four coins. By how much is the total number of coins in the magical forest greater than the number of trees?
|
Let $x$ be the number of trees in the forest on which three coins grow, and on which one coin grows. Then in the forest, $2 x$ trees do not grow any coins at all.
Thus, the total number of coins is
$$
2 x \cdot 0+y \cdot 1+3 \cdot 2+x \cdot 3+4 \cdot 4=3 x+y+22
$$
and the total number of trees is
$$
2 x+y+3+x+4=3 x+y+7
$$
The first number is 15 more than the second.
|
15
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{15}\)
|
Problem 5.6. In the zoo, there are red, yellow, and green parrots (there is at least one parrot of each of the listed colors; there are no parrots of other colors in the zoo). It is known that among any 10 parrots, there is definitely a red one, and among any 12 parrots, there is definitely a yellow one. What is the maximum number of parrots that can be in the zoo?
|
Let there be $x$ red, $y$ yellow, and $z$ green parrots in the zoo.
Since among any 10 parrots there is a red one, the number of non-red parrots does not exceed 9, that is, $y+z \leqslant 9$. By similar reasoning, we get that the number of non-yellow parrots does not exceed 11, that is, $x+z \leqslant 11$.
Thus,
$$
\begin{gathered}
x+y+2 z=(y+z)+(x+z) \leqslant 9+11=20 ; \\
x+y+z \leqslant 20-z \leqslant 19
\end{gathered}
$$
This means that the total number of parrots does not exceed 19. At the same time, there could have been 10 red, 8 yellow, and 1 green parrot in the zoo, that is, exactly 19 parrots.
|
19
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{19}\)
|
8.2. Borya found the smallest prime number \( p \) such that \( 5 p^{2} + p^{3} \) is a square of some natural number. What number did Borya find?
|
Since $5 p^{2}+p^{3}=p^{2}(5+p)$, the original number is a perfect square if and only if the number $5+p$ is a perfect square. Since $p$ is a prime number, $p+5 \geq 7$. It is sufficient to verify that if $p+5=9$, then $p=4$ is not a prime; if $p+5=16$, then $p=11$ satisfies the condition, and this value of $p$ will be the smallest.
Note: The problem can also be solved by sequentially checking prime numbers starting from $p=2$. Criteria: Only the answer (including verification) - 0 points. Correct answer with a correct solution (including finding by checking all (!) primes $p$ up to 11) - 7 points. The problem is reduced to the fact that $(5+p)$ is a prime number, but not completed or further with an error - 3 points.
|
11
|
Number Theory
|
olympiads
| null | null |
\(\boxed{11}\)
|
Problem 6.1. The set includes 8 weights: 5 identical round, 2 identical triangular, and one rectangular weight weighing 90 grams.
It is known that 1 round and 1 triangular weight balance 3 round weights. Additionally, 4 round weights and 1 triangular weight balance 1 triangular, 1 round, and 1 rectangular weight.
How much does the triangular weight weigh?
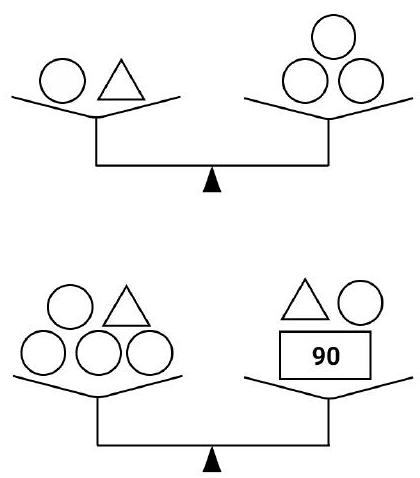
|
From the first weighing, it follows that 1 triangular weight balances 2 round weights.
From the second weighing, it follows that 3 round weights balance 1 rectangular weight, which weighs 90 grams. Therefore, a round weight weighs $90: 3=30$ grams, and a triangular weight weighs $30 \cdot 2=60$ grams.
|
60
|
Algebra
|
olympiads
| null | null |
\(\boxed{60}\)
|
11.1. A unified control test in mathematics was conducted among all eleventh-graders in the school. As a result, 5/8 of the students received fives, 11/20 of the number of excellent students received fours, and the remaining three eleventh-graders did not come to the test due to illness. How many eleventh-graders are there in the school
|
The share of students who received fours is 55/160. The share of students who received fives and fours is $5 / 8 + 55 / 160 = 155 / 160$. Thus, the share of students who missed the exam is $5 / 160 = 1 / 32$. Let $N-$ be the number of eleventh graders, then from the condition $N / 32 = 3$ and $N = 96$.
|
96
|
Algebra
|
olympiads
| null | null |
\(\boxed{96}\)
|
1. Masha left the house for school. A few minutes later, Vanya ran out of the same house to school. He overtook Masha at one-third of the way, and when he arrived at school, Masha still had half of the way left to go. How many times faster does Vanya run compared to how Masha walks?
|
At one third of the way, Masha and Vanya were at the same time. After that, Vanya ran $2 / 3$ of the way, while Masha walked $1 / 2 - 1 / 3 = 1 / 6$ of the way in the same time. This means that he runs $2 / 3$ : $1 / 6 = 4$ times more in the same amount of time than Masha.
|
4
|
Algebra
|
olympiads
| null | null |
\(\boxed{4}\)
|
1. Real numbers $a, b, c$ are such that $a+1 / b=9, b+1 / c=10$, $c+1 / a=11$. Find the value of the expression $a b c+1 /(a b c)$.
|
Sketch of the solution. By multiplying the equations, expanding the brackets, and grouping, we get: $a b c + 1/(a b c) + a + 1/b + b + 1/c + c + 1/a = 990$. From this, $a b c + 1/(a b c) = 990 - 9 - 10 - 11 = 960$.
|
960
|
Algebra
|
olympiads
| null | null |
\(\boxed{960}\)
|
8.4. It is known that for real numbers $a$ and $b$ the following equalities hold:
$$
a^{3}-3 a b^{2}=11, \quad b^{3}-3 a^{2} b=2
$$
What values can the expression $a^{2}+b^{2}$ take?
|
We have
$$
\left(a^{2}+b^{2}\right)^{3}=a^{6}+3 a^{4} b^{2}+3 a^{2} b^{4}+b^{6}=\left(a^{3}-3 a b^{2}\right)^{2}+\left(b^{3}-3 a^{2} b\right)^{2}=11^{2}+2^{2}=125
$$
From this, $a^{2}+b^{2}=5$.
Comment. A correct and justified solution - 7 points. The correct answer obtained based on a simple example satisfying the condition ( $a=-1, b=2$ ), but not proven that the same answer for other pairs - 3 points. Some progress - 2 points. The solution is started, but the progress is insignificant - 1 point. Only the answer is provided - 0 points. The problem is not solved or solved incorrectly - 0 points.
|
5
|
Algebra
|
olympiads
| null | null |
\(\boxed{5}\)
|
5. Every day in November, Winnie-the-Pooh visited either Piglet, or Rabbit, or Eeyore. For any two consecutive days, he visited Piglet at least once, and for any three consecutive days, he visited Rabbit at least once. How many times could he have visited Eeyore during this time? (November has 30 days. Winnie-the-Pooh visited Eeyore at least once).
|
Suppose Winnie-the-Pooh visited Eeyore on some day in November, but not on the 1st or the 30th. Since over any two consecutive days he visited Piglet at least once, he must have visited Piglet the day before visiting Eeyore, and he must also have visited Piglet the day after visiting Eeyore. This means that over these three consecutive days, he did not visit Rabbit at all, which contradicts the condition. Therefore, Winnie-the-Pooh could visit Eeyore no more than twice (only on the 1st and the 30th of November). We will show that he could visit Eeyore once or twice. Let visits to Rabbit be denoted by K, to Piglet by P, and to Eeyore by I.
He could visit Eeyore once in the following way: IPKPK...PKP. He could visit Eeyore twice in the following way: IPKPPP...PKPKP...PKPI.
|
2
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{2}\)
|
4. Solve the following equation for positive $x$.
$$
x^{2014} + 2014^{2013} = x^{2013} + 2014^{2014}
$$
|
Rewrite the equation in the following form $x^{2013}(x-1)=2014^{2013}(2014-1)$. The solution is $x=2014$. Since the function on the left, for $x>1$ this function is increasing, as the product of two positive increasing functions, the intersection with a constant function can be no more than one and one is already defined.
## Grading Criteria.
The solution is guessed: 0 points.
|
2014
|
Algebra
|
olympiads
| null | null |
\(\boxed{2014}\)
|
4.4. In a $3 \times 4$ rectangle, natural numbers $1,2,3, \ldots, 12$ were written, each exactly once. The table had the property that in each column, the sum of the top two numbers was twice the bottom number. Over time, some numbers were erased. Find all possible numbers that could have been written in place of $\star$.
| 6 | | | |
| :--- | :--- | :--- | :--- |
| 4 | | | |
| | 8 | 11 | $\star$ |
Answer, variant 1. 11.
Answer, variant 2. 8.
Answer, variant 3. 11.
Answer, variant 4. 2.
|
According to the condition, the number 2 is written in the bottom-left cell. The sum of the two unknown numbers in the second column is 10, and in the third column, it is 16. Therefore, the sum of the numbers in the first three columns is $6+15+24$, and the sum of all numbers in the table is $1+2+\ldots+12=78$. Thus, the sum of the numbers in the fourth column is $78-6-15-24=33$. From the condition, it follows that the number at $\star$ is one-third of 33, which is 11.
Remark. The arrangement of numbers described in the condition is indeed possible. For example, such an arrangement:
| 1 | 6 | 9 | 10 |
| :--- | :--- | :--- | :--- |
| 3 | 4 | 7 | 12 |
| 2 | 5 | 8 | 11 |
|
11
|
Logic and Puzzles
|
olympiads
| null | null |
\(\boxed{11}\)
|
8.4. Sasha is a coffee lover who drinks coffee at work, so every morning before work, he prepares a thermos of his favorite drink according to a strict ritual. He brews 300 ml of the strongest aromatic coffee in a Turkish coffee pot. Then Sasha repeats the following actions 6 times: he pours 200 ml from the pot into the thermos, and adds 200 ml of water to the pot, and mixes thoroughly. After the 6th time, Sasha pours all 300 ml from the pot into the thermos. What will be the concentration of the original strongest aromatic coffee in the thermos? Initially, the thermos is empty.
The concentration is a number from 0 to 1. Provide the answer as a fraction (common or decimal), not as a percentage.
Answer, option 1. 0.2 .
Answer, option 2. 0.2 .
Answer, option 3.0 .2 .
Answer, option 4. 0.2 .
|
option 1. Note that by the end of the ritual, there will be 200 ml of coffee and 800 ml of water in the thermos. Therefore, the concentration of coffee is $200 / 1000 = 1 / 5 = 0.2$.
Remark. One could try to solve the problem "step by step": calculate the concentration of coffee in the thermos after the first transfer, after the second, and so on. With such an approach, complex expressions are obtained, and the probability of solving the problem correctly is minimal.
|
0.2
|
Other
|
olympiads
| null | null |
\(\boxed{0.2}\)
|
2. In a beach soccer tournament, 17 teams participate, and each team plays against each other exactly once. Teams are awarded 3 points for a win in regular time, 2 points for a win in extra time, and 1 point for a win on penalties. The losing team does not receive any points. What is the maximum number of teams that can accumulate exactly 5 points?
|
Sketch of the solution. Estimation. Let $n$ teams have scored exactly 5 points each. The total points include all points scored by these teams in matches against each other (at least 1) and possibly in matches against other teams: $5 n \geq(n-1) n / 2$. Hence, $n \leq 11$.
Example: Place eleven teams in a circle, and let each team win against the five teams following them in a clockwise direction by penalty. The remaining teams lost to them.
Criteria. Example without estimation: 2 points. Estimation without example: 4 points.
|
11
|
Combinatorics
|
olympiads
| null | null |
\(\boxed{11}\)
|
10.1. Find the number of roots of the equation
$$
|x|+|x+1|+\ldots+|x+2018|=x^{2}+2018 x-2019
$$
(V. Dubinskaya)
|
For $x \in(-2019,1)$ there are no roots, since on the given interval the left side is non-negative, while the right side is negative.
For $x \in[1, \infty)$ all absolute values are resolved with a positive sign, so the equation will take the form $g(x)=0$, where $g(x)=x^{2}-x-2009+(1+2+\ldots+2018)$. Since $g(1)<0$, this quadratic equation has a single root on the interval $[1, \infty)$.
Since the graphs of the functions on the left and right sides are symmetric with respect to the line $x=-1009$ (i.e., $f(x)=f(-2018-x)$), there are as many roots on the interval $(-\infty,-2019]$ as there are on the interval $[1,+\infty)$, i.e., exactly one root. In total, the given equation has two roots.
|
2
|
Algebra
|
olympiads
| null | null |
\(\boxed{2}\)
|
# 3. The numbers $2^{2021}$ and $5^{2021}$ are written one after another. How many digits are written in total?
#
|
# Solution
Let the number $2^{2021}$ have $\mathrm{k}$ digits, and the number $5^{2021}$ have $\mathrm{m}$ digits, then the number of digits in the desired number is $\mathrm{k}+\mathrm{m}$. $10^{k-1}<2^{2021}<10^{k}, 10^{m-1}<5^{2021}<10^{m}$, therefore, $10^{k+m-2}<$ $10^{2021}<10^{m+k}$ and $\mathrm{k}+\mathrm{m}=2022$.
## Evaluation Criteria
The solution includes intermediate estimates that allow reaching the required estimate - from 13 points depending on the progress in the solution.
An incorrect answer due to a logical error - from 1-4 points depending on the progress in the solution.
An incorrect answer due to a computational error - 5 points.
A correct result obtained with justification - 7 points.
|
2022
|
Number Theory
|
olympiads
| null | null |
\(\boxed{2022}\)
|
9.1. Four non-zero numbers are written on the board, and the sum of any three of them is less than the fourth number. What is the smallest number of negative numbers that can be written on the board? Justify your answer.
|
Let the numbers on the board be $a \geqslant b \geqslant c \geqslant d$. The condition of the problem is equivalent to the inequality $a+b+c < d$ for optimality | 7 points |
| There is a proof that there are no fewer than three negative numbers (in the absence of an example with three numbers) | 3 points |
| An example of a set with three negative numbers is provided (in the absence of a proof of its optimality) | 1 point |
| Correct answer without justification (or with incorrect justification) | 0 points |
| Examples of sets with four negative numbers | not evaluated |
|
3
|
Inequalities
|
olympiads
| null | null |
\(\boxed{3}\)
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.